Graphing Exponential Functions and their Transformations
Graphs of Exponential Functions
The graphs of exponential functions and their shape (along with locations of the “control points”) are entirely dictated by the base of the exponential function. Below we illustrate the key differences along with some of the key features of these two sorts of graphs. This will augment our library of functions considerably!
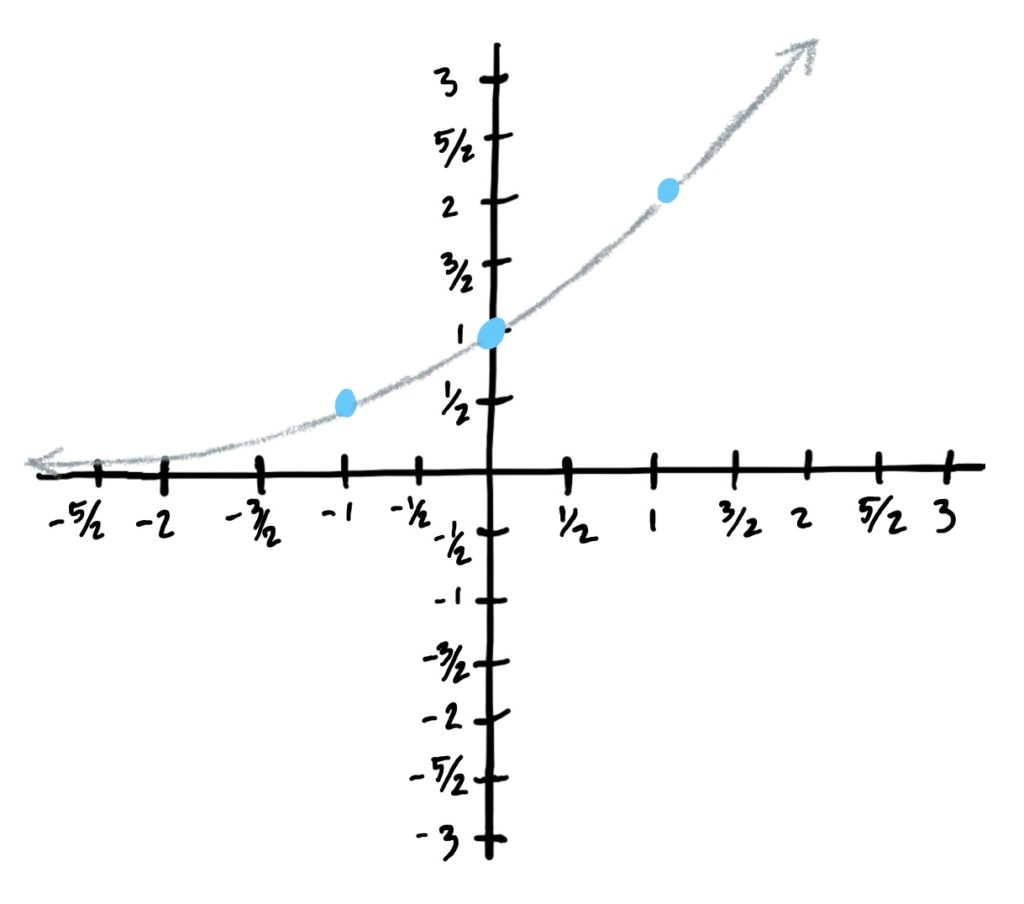
\(f(x)=a^x\) where \(a>1\)
Key Features:
- The graph will NEVER cross the \(x\)-axis, but it will get as close as you like to it from above as \(x\) gets more and more negative. This gives a horizontal asymptote at \(y=0\).
- As \(x\)-value inputs get bigger, the \(y\)-values explode into the sky (i.e. increase quickly).
Control/Reference Points
The graph of \(f(x)=a^x\) passes through \((-1,\frac{1}{a})\), \((0,1)\), and \((1,a)\).
The graph at left shows the function \(f(x)=2^x\) which has control points \((-1,\frac{1}{2}), (0,1),\) and \((1,2)\).
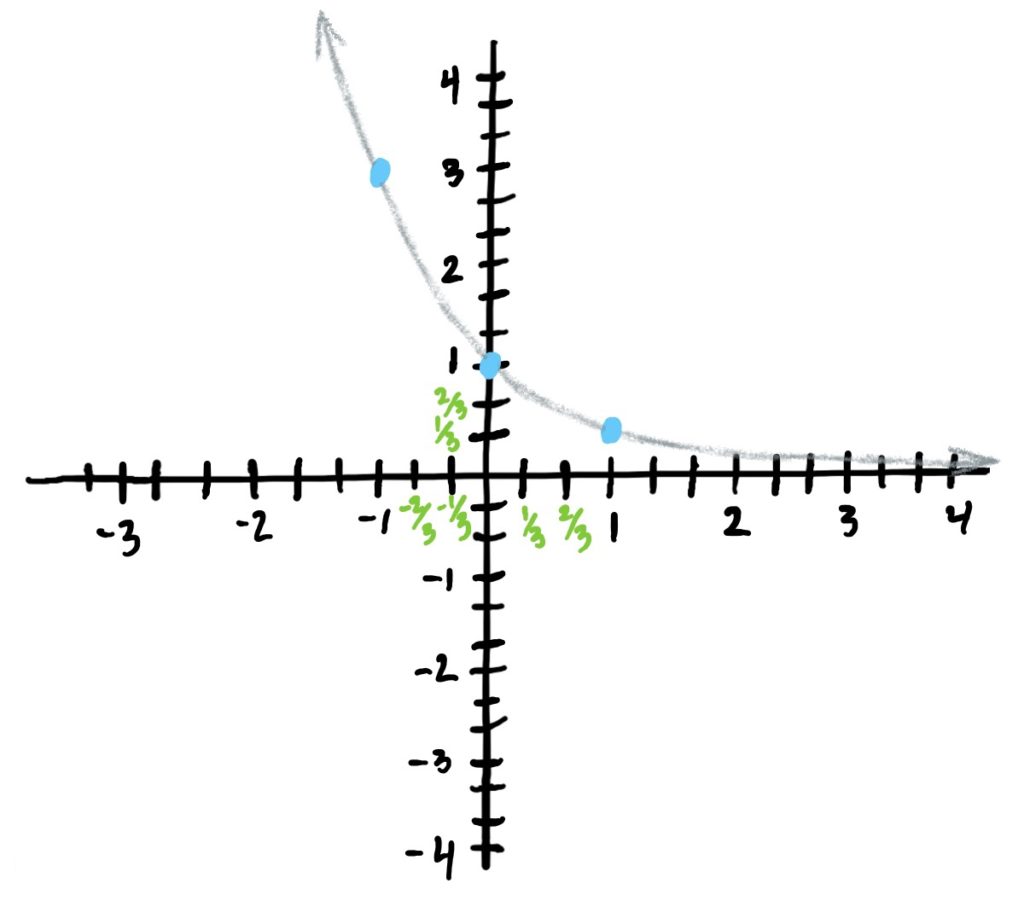
\(f(x)=a^x\) where \(a<1\)
Key Features:
- The graph will NEVER cross the \(x\)-axis, but it will get as close as you like to it from above as \(x\) gets more and more positive. This gives a horizontal asymptote at \(y=0\).
- As \(x\)-value inputs get bigger, the \(y\)-values decrease more slowly, tending toward \(y=0\).
Control/Reference Points
The graph of \(f(x)=a^x\) passes through \((-1,a)\), \((0,1)\), and \((1,\frac{1}{a})\).
The graph at right is the graph of the function \(f(x)=\left(\frac{1}{3}\right)^x\), which has control points \((-1,3), (0,1), (1,\frac{1}{3})\)
To reiterate the above, the graph and thus the control points used to graph an exponential are largely determined by the base \(a\). It’s helpful to try listing the control points of functions of the form \(f(x)=a^x\) for different \(a\)-values so that you see a pattern in how they are computed. Note that regardless of whether \(a>1\) or \(a<1\), the control points are calculated the same way. See below.
| Exponential Function | \(a\)-value (base) | Control Points: \((-1,\frac{1}{a})\), \((0,1)\), \((1,a)\) |
| \(f(x)=\left(\frac{1}{3}\right)^x\) | \(a=\frac{1}{3}\) | \((-1,3)\), \((0,1)\), \((1,\frac{1}{3})\) |
| \(f(x)=\left(\frac{1}{2}\right)^x\) | \(a=\frac{1}{2}\) | \((-1,2)\), \((0,1)\), \((1,\frac{1}{2})\) |
| \(f(x)=\left(\frac{2}{3}\right)^x\) | \(a=\frac{2}{3}\) | \((-1,\frac{3}{2})\) (because \(\frac{1}{\frac{2}{3}}=\frac{3}{2}\)), \((0,1)\), \((1,\frac{2}{3})\) |
| \(f(x)=2^x\) | \(a=2\) | \((-1,\frac{1}{2})\), \((0,1)\), \((1,2)\) |
| \(f(x)=5^x\) | \(a=5\) | \((-1,\frac{1}{5})\), \((0,1)\), \((1,5)\) |
Transforming Exponential Functions
Function transformations performed on exponential functions work exactly the same way as any other function:
- To shift the function horizontally, add or subtract a constant to/from \(x\) up in the exponent.
- To scale the function horizontally, multiply \(x\) in the exponent by a constant.
- To flip/reflect the function over the \(y\)-axis, multiply \(x\) in the exponent by a negative number.
- To scale/stretch or compress vertically, multiply the whole function by a constant.
- To flip/reflect the function over the \(x\)-axis, multiply the exponential expression by a negative number.
- To shift the function vertically up or down, add or subtract a constant (number) to/from the whole entire function.

First find the control points and plot those. The control points are \((-1,\frac{1}{3})\), \((0,1)\), \((1,3)\). Since the base is greater than \(1\), the \(y\)-values of the function increase as the input \(x\)-values increase. This gives the graph the shape you see below once you draw through the plotted control points. Note that the graph has a horizontal asymptote at \(y=0\); i.e. it doesn’t cross the \(x\)-axis EVER!


First find the control points and plot those. The control points are \((-1,5)\), \((0,1)\), \((1,\frac{1}{5})\). Since the base is less than \(1\), the \(y\)-values of the function decrease as the input \(x\)-values increase. This gives the graph the shape you see below once you draw through the plotted control points. Note that the graph has a horizontal asymptote at \(y=0\); i.e. it doesn’t cross the \(x\)-axis EVER!


First find the control points and plot those. The control points are \((-1,\frac{5}{3})\) (because \(\frac{1}{\frac{3}{5}}=\frac{5}{3}\) by keep-change-flip method), \((0,1)\), \((1,\frac{3}{5})\). Since the base is less than \(1\), the \(y\)-values of the function decrease as the input \(x\)-values increase. This gives the graph the shape you see below once you draw through the plotted control points. Note that the graph has a horizontal asymptote at \(y=0\); i.e. it doesn’t cross the \(x\)-axis EVER!

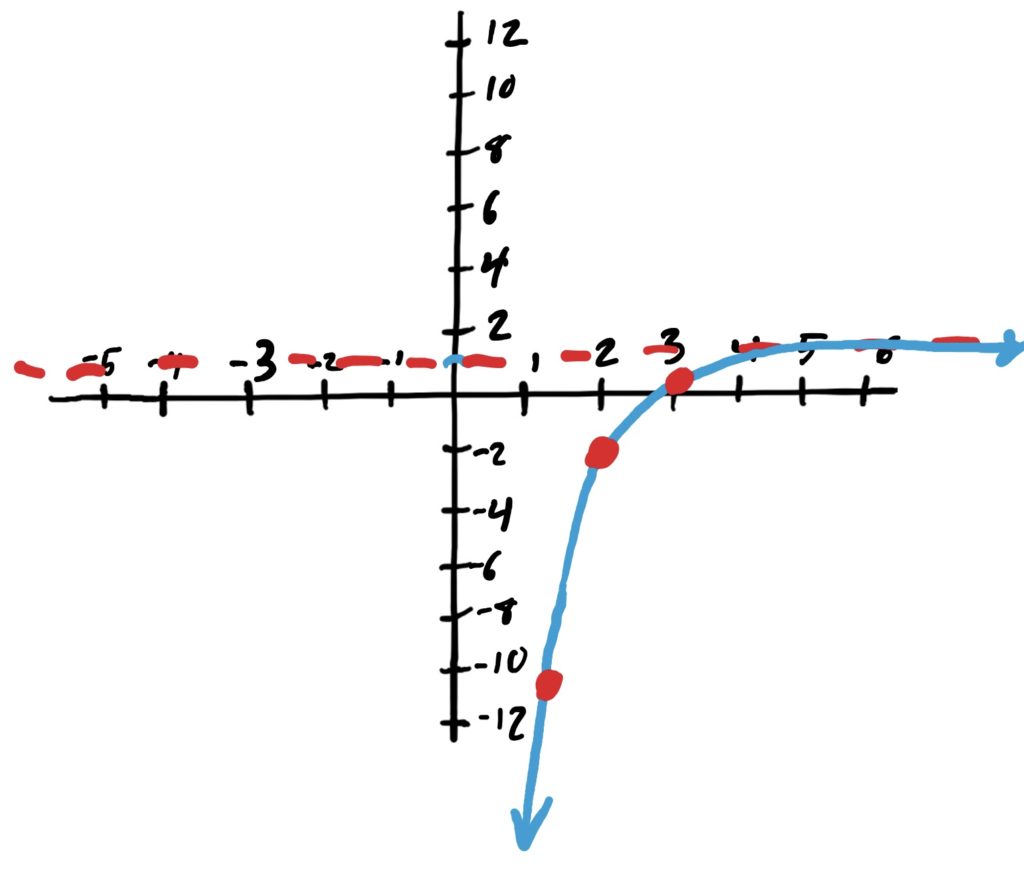
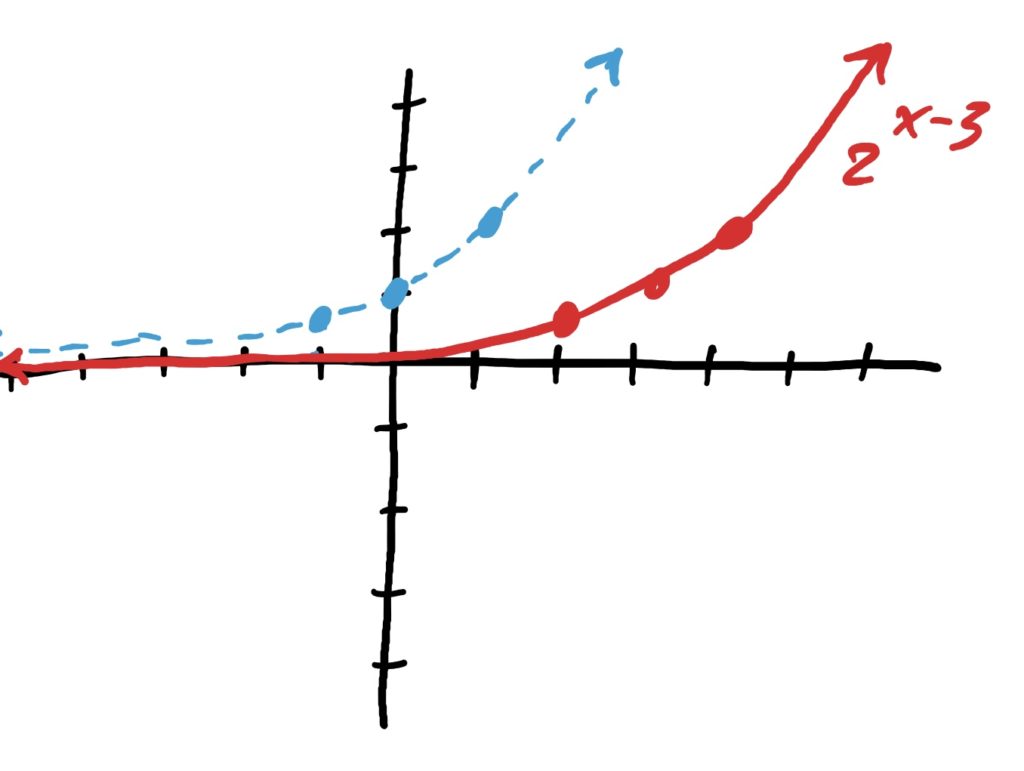
Library Simple Exponential Function: \(2^x\)
Transformations: Shifted right by 3
Final Graph below
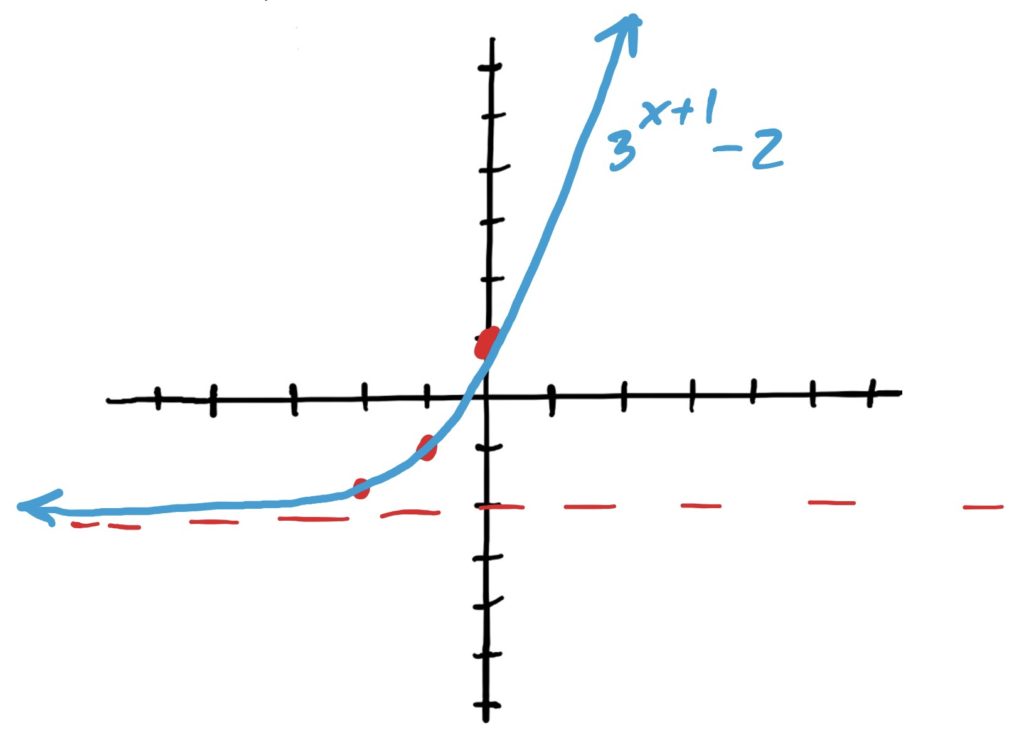
Library Simple Exponential Function: \(3^x\)
Transformations Applied: Shifted left 1, down 2
Final Graph:
Library Simple Exponential Function: \(\left(\frac{1}{2}\right)^{x}\)
Transformations Applied: Shifted right by 1, then up 3.
Final Graph:
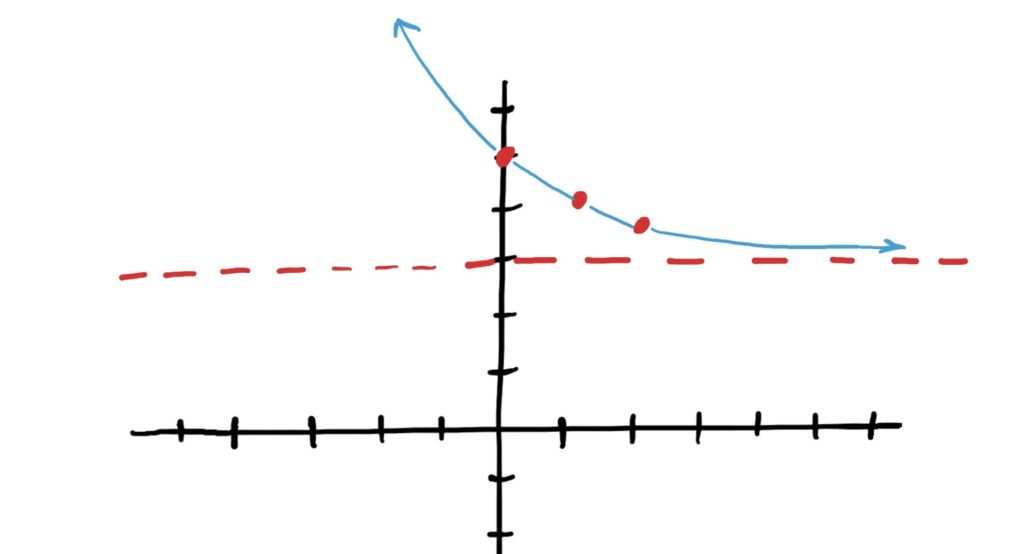
Simple Exponential Function: \(\left(\frac{1}{2}\right)^x\)
Transformations Applied: Shifted right 3, then scaled vertically by 3
Final Graph:
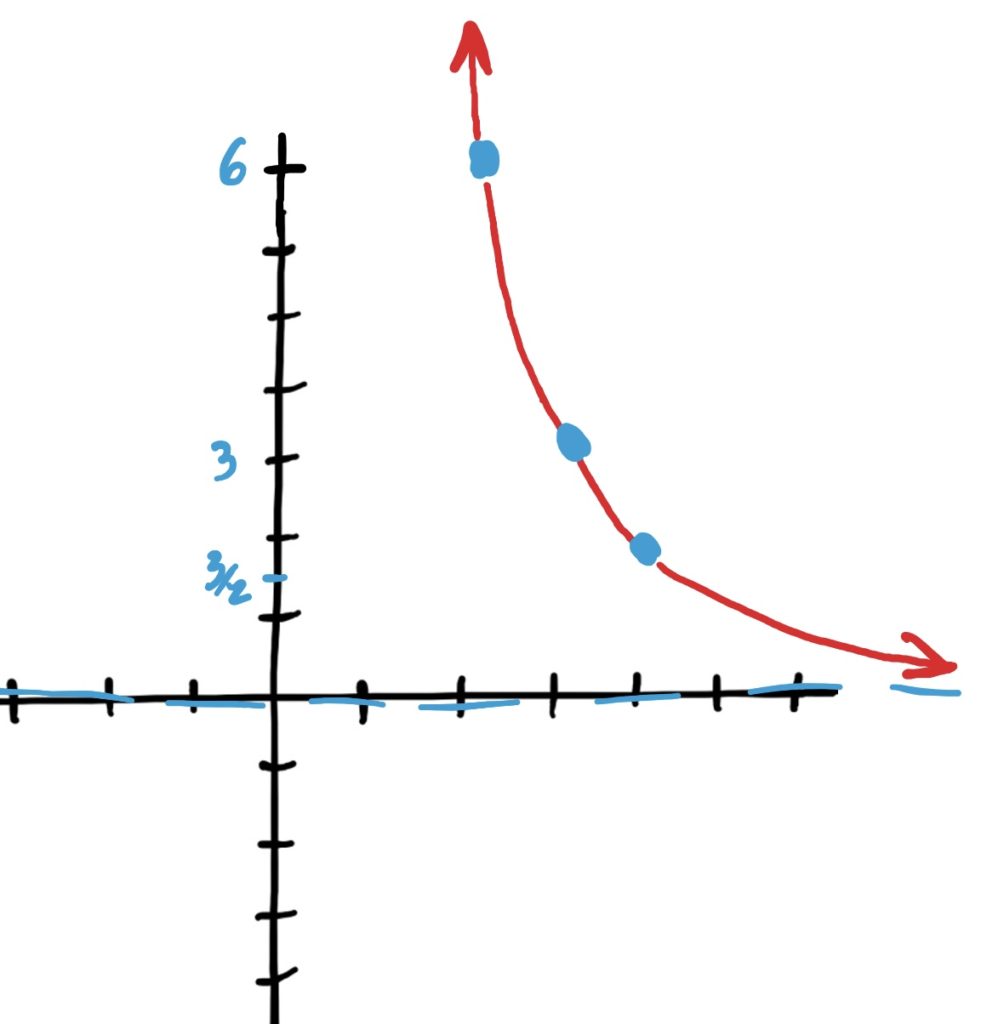
Simple Exponential Function: \(2^x\)
Transformations Applied: Shifted right by 3, reflected horizontally over \(y\)-axis, then compressed (scaled) vertically by \(\frac{1}{3}\).
Final Graph:
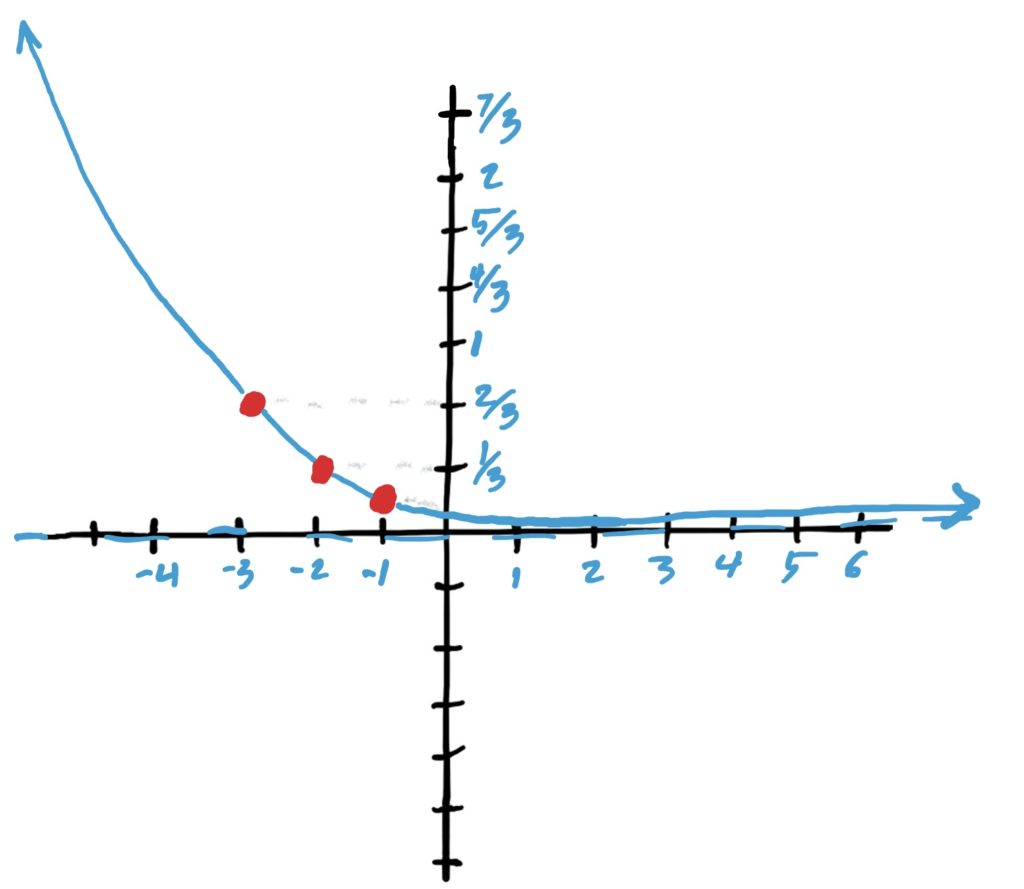
Simple Exponential Function: \(4^x\)
Transformations Applied: shifted left by 2, reflected over \(y\)-axis, scaled vertically by \(3\), reflected over the \(x\)-axis, then shifted up by \(1\).
Final Graph: