$Project Greater Ed Logo$

The Difference Quotient

Precalculus Algebra The Difference Quotient

Difference Quotient

Let $f$ be a function. The difference quotient of $f$ is the expression
$$\begin{align} \frac{f(x+h)-f(x)}{h}\end{align}$$
where $x, h$ are variables representing real numbers.

This expression is a variabnt of an average rate of change (i.e. slope, or rise over run) of the function $f$ when the difference between the start $x$-value and the end $x$-value is $h$. If this made no sense, don’t worry about it, since it is not your problem…. yet.

Difference quotients are used in the formulation of derivatives in Calculus, simplify by taking (what is called) a limit “as $h$ approaches $0$.”

Simplifying difference quotients causes trouble for students all the way up through Calc 3, so we practice doing them here to save you many points later!

Simplifying Difference Quotients

Let $f$ be a function. To compute the difference quotient
$$\frac{f(x+h)-f(x)}{h}$$
1.) First find $f(x+h)$ by replacing all the $x$’s you see in the rule for $f$ with the expression $(x+h)$. Then Expand/Distribute/FOIL if possible.

2.) Using your answer from the last bullet, compute $f(x+h)-f(x)$ by subtracting the rule for $f$ from the answer you got in the last bullet.

3.) To compute the final result, namely $\frac{f(x+h)-f(x)}{h}$, divide the answer you got to the last bullet by $h$, and factor an $h$ out of the numerator to cancel the one in the denominator. Alternatively, you can distribute the fraction.

Following the instructions above, start by computing $f(x+h)$ by plugging the whole quantity $(x+h)$ into the rule for $f$, every place you see an $x$:

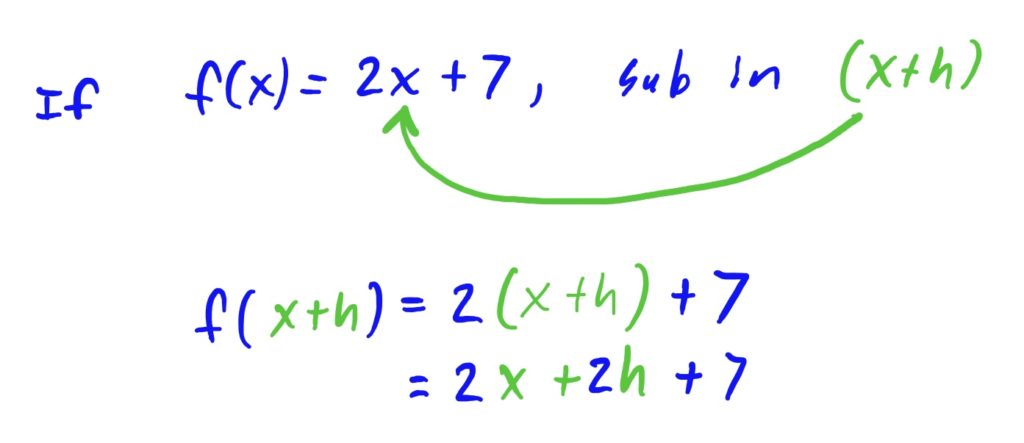
Now, for step 2, take the rule for $f(x)$ and subtract it from what you got above:

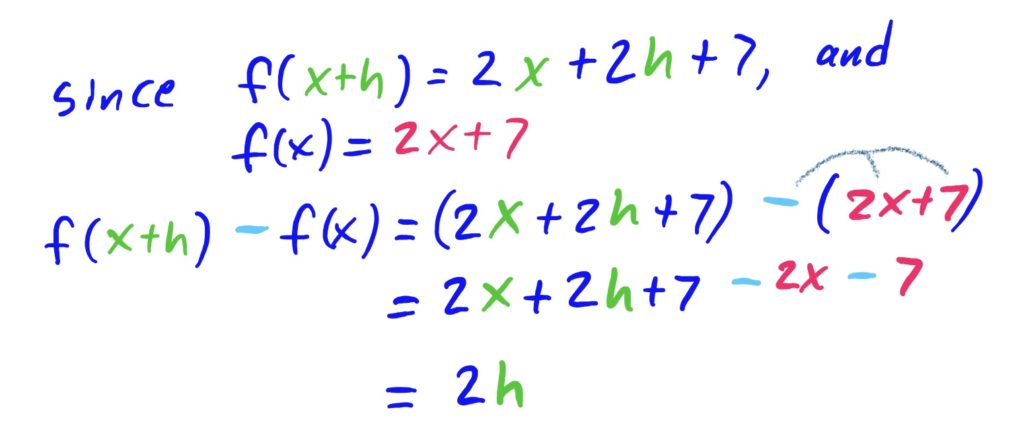
Lastly, to find the final answer for $\frac{f(x+h)-f(x)}{h}$, take the last answer and divide by $h$, then simplify by cancelling (normally will need to factor the numerator, but here there is no need).

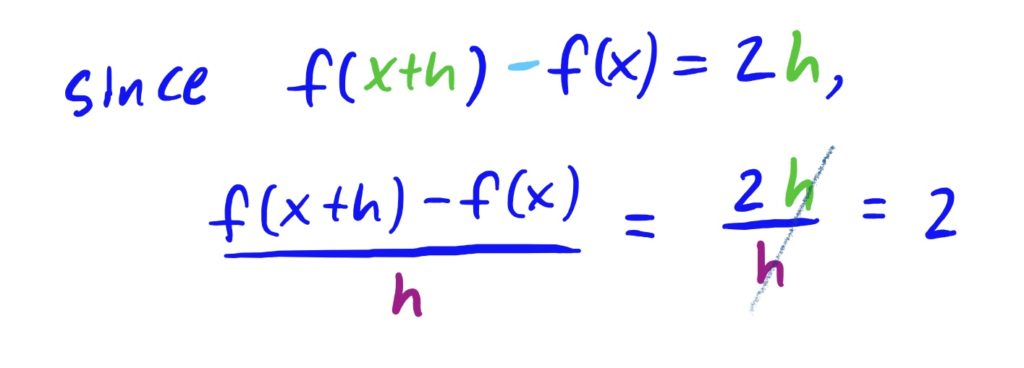
Done!

Following these steps as shown above, and being verrrrry careful in your algebra gymnastics will help you solve difference quotient problems, and impress your Calculus instructor when derivatives are first introduced.

$$\frac{f(x+h)-f(x)}{h}$$

$3$

$$\frac{f(x+h)-f(x)}{h}$$

$$\frac{f(x+h)-f(x)}{h}=2x+h$$

$$\frac{f(x+h)-f(x)}{h}$$

$$\frac{f(x+h)-f(x)}{h}=3x^2+3xh+h^2$$

$$\frac{f(x+h)-f(x)}{h}$$

$$\frac{f(x+h)-f(x)}{h}=\frac{-1}{x(x+h)}$$

$$\frac{f(x+h)-f(x)}{h}$$

$$\frac{f(x+h)-f(x)}{h}=\frac{1}{\sqrt{x+h}+\sqrt{x}}$$

$$\frac{f(x+h)-f(x)}{h}=\frac{\sqrt{x+h}-\sqrt{x}}{h}$$

Previous Lesson

Back to Course

Next Lesson