$Project Greater Ed Logo$

Combinations

In the last lesson, we talked about permutations which are nothing more than arrangements of some collection of objects (usually taken from a bigger collection of objects). We considered permutations when counting the number of ways we could select objects to fill first, second, third, etc. For instance, if Alice, Bob, and Cathy get first, second, and third, respectively, in a race involving 200 people, this is a very different outcome from Bob getting first, Cathy getting second, and Alice getting third place, even though the same three people placed in the top three. In other words, the order matters when counting permutations.

When selecting a subcollection of objects from a larger collection, but where the order doesn’t matter, what we have is called a combination. The following formula helps us compute the total number of combinations of $m$ objects selected from a larger collection of $n$ objects.

Number of Ways of Selecting $m$ Objects from a Set of $n$

The number of ways of selecting $m$ objects from a larger collection of $n$ objects, denoted by either
$$\begin{align} _nC_m\ \ or\ \ \binom{n}{m} \end{align}$$
and pronounced “$n$ choose $m$”, is given by the formula
$$\begin{align} _nC_m=\binom{n}{m}=\frac{n!}{m!\cdot (n-m)!}\end{align}.$$

Let’s first look at a situation in which this formula could be used.

Here, the order of the committee members does not matter. That is, it doesn’t matter who is selected first, second, third, etc. for the committee. All that matters is which of the 104 faculty are on this committee of $25$. The total number of combinations of $25$ committee members out of a total of $104$ is given by

$$\begin{align} \binom{104}{25} &= \frac{104!}{25!\cdot (104-25)!}\\&=\frac{104!}{25!\cdot 79!}\\&=742185302773239315585504\end{align}$$

What to Watch For

When dealing with permutations, order matters. So situations where you are reorganizing or re-ordering objects typically are permutation problems.

When dealing with combinations, order does not matter. Combinations are usually indicated by needing to select a certain number of objects from a larger collection, without any regard to the order in which they are selected.

Sometimes combination problems are disguised as permutation problems and vice versa. Drawing pictures or carefully turning the situation/problem over in your mind usually helps you determine which type of problem you are dealing with.

Why the Formula Works

Let’s look at this within the context of a problem and leverage what we know about permutations.

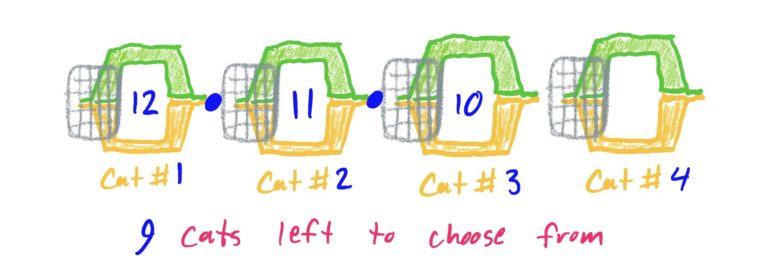
Question: Suppose I visit the animal shelter knowing that I will leave with 4 cats. The shelter currently houses $12$ cats to choose from. How many different combinations of cats could I leave the shelter with?

Using a “slots” approach, as with permutations, we have four slots (or, if you prefer, cat carriers) that we can fill with different cats, and we have 12 cats to choose from for the first slot/carrier. Then, for each of the 12 cats I could select for the first slot/carrier, after choosing one, I have 11 remaining cats to choose from for the second slot/carrier. Similarly, for the third and fourth slot/carrier, I can choose from 10 and 9 cats, respectively. This is depicted below.

However, the above computation takes into consideration the order I am choosing these cats in. For instance, choosing cats in the order “Meeko,” then “Totoro,” then “Peanut,” then “Orzo” is different from choosing “Totoro” first and then “Meeko,” then “Peanut,” then “Orzo.”

Since it doesn’t matter which cat I pick first, second, third, or fourth (I’m taking the same collection of cats home regardless of the order I chose them in), and because the above computation takes into consideration the order of the four cats that would be chosen, I need to remove (the double-count of) all the different rearrangements of every collection of four cats I could choose.

So, since there are $_{12}P_4=\frac{12!}{(12-4)!}=12\cdot 11\cdot 10\cdot 9$ ways of choosing four cats out of $12$ to fill a first, second, third, and fourth carrier/slot, and since there are $4\cdot 3\cdot 2\cdot 1=4!$ ways of reordering these cats into these $4$ different carriers/slots once they’ve been chosen, the total number of ways I can choose $4$ cats out of $12$ (without caring which order or carriers/slots they come in) is found by dividing the above computation by $4!$. Viz:

$$\frac{_{12}P_4}{4!}=\frac{12\cdot 11\cdot 10\cdot 9}{4!}=\frac{\frac{12!}{(12-4)!}}{4!}=\frac{12!}{4!\cdot(12-4)!}$$

But this matches what the combination formula gives, namely $\binom{12}{4}=\frac{12!}{4!\cdot(12-4)!}$. The following observation generalizes this concept.

Observation

$$\binom{n}{m} =\frac{_nP_m}{m!}=\frac{n!}{m!(n-m)!}$$

Try some of the examples below. Apply the formulas where appropriate, and avoid the temptation to force problems to work out a certain way, or the same way as examples you’ve seen before. Some of the problems might require the use of the combination formula several times! All in all, just be sure to very carefully consider the situation given in the problem. You have all the tools you need, just need to be wise about how you use them.

$\binom{5}{3}=10$

$\binom{10}{7}=120$

$\binom{5}{3}=\frac{5!}{3!\cdot (5-3)!}=\frac{5!}{3!\cdot 2!}=10$

$\binom{10}{7}=\frac{10!}{7!\cdot (10-7)!}=\frac{10!}{7!\cdot 3!}=120$

Recall that $0!=1$.

$\binom{3}{3}=1$

$\binom{6}{6}=1$

$\binom{n}{n}=1$

$\binom{3}{3}=\frac{3!}{3!\cdot (3-3)!}=\frac{3!}{3!\cdot 0!}=\frac{3!}{3!}=1$

$\binom{6}{6}=\frac{6!}{6!\cdot (6-6)!}=\frac{6!}{6!\cdot 0!}=\frac{6!}{6!}=1$

$\binom{n}{n}=\frac{n!}{n!\cdot (n-n)!}=\frac{n!}{n!\cdot 0!}=\frac{n!}{n!}=1$

$\binom{n}{1}=n$

Notice that by our formula,

$$\begin{align}\binom{n}{1}&=\frac{n!}{1!\cdot (n-1)!}\\&=\frac{n\cdot (n-1)\cdot (n-2)\cdot (n-3)\cdot …\cdot 2\cdot 1}{(n-1)\cdot (n-2)\cdot (n-3)\cdot…\cdot 3\cdot 2\cdot 1}\\&=\frac{n}{1}\\&=n\end{align}$$

where the big fraction got reduced by cancelling the same terms in the numerator and denominator.

Recall that $0!=1$.

$\binom{n}{0}=1$

Notice that $\binom{n}{0}=\frac{n!}{0!\cdot (n-0)!}=\frac{n!}{1\cdot n!}=1$.

$\binom{30}{4}=\frac{30!}{4!\cdot(26)!}=27405$

There are $30$ club members to select $4$ from, and since we are forming a committee, it really doesn’t matter in which order these committee members are selected. So we have a combination problem, and the number of combinations we have total is given in the answer above.

Don’t go listing out subsets!

$\binom{4}{3}=\frac{4!}{3!\cdot 1!}=4$

There are $4$ elements in the set to choose from when forming a subset of order $3$. Since order doesn’t matter when writing elements in set notation, this forms a combination. So we have a total of $\binom{4}{3}$ possible subsets of order $3$.

Interesting note: This result can also be obtained by determining the number of ways of omitting one element from the set, as opposed to including $3$ out of the $4$.

Don’t go listing out subsets!

$\binom{7}{4}=\frac{7!}{4!\cdot 4!}=35$

There are $7$ elements in the set to choose from when forming a subset of order $4$. Since order doesn’t matter when writing elements in set notation, this forms a combination. So we have a total of $\binom{7}{4}$ possible subsets of order $4$.

$$\begin{align}\binom{6}{3}\cdot \binom{4}{2}&=\frac{6!}{3!\cdot(6-3)!}\cdot \frac{4!}{2!\cdot(4-2)!}\\&=\frac{6!}{3!\cdot3!}\cdot \frac{4!}{2!\cdot 2!}\\&=20\end{align}$$

There are $\binom{6}{3}$ ways one can choose three blue marbles from the total of six blue marbles. Since we don’t want any more blue marbles in the two additional marbles we select, we are limited to selecting the remaining two marbles from the stash of red ones. There are $\binom{4}{2}$ ways of selecting $2$ red marbles from a stash of $4$ red marbles. So for each choice of three blue marbles, there are $\binom{4}{2}$ choices for red marbles, leading to a total of $\binom{6}{3}\cdot \binom{4}{2}=20$ possible combinations.

$\binom{8}{3}\cdot\binom{10}{1}=560$

There are $\binom{8}{3}$ ways of selecting three red marbles from the $8$ possible red marbles. Then, for each choice/combination of red marbles, since three marbles have been chosen, there are ten marbles remaining from which we choose the single fourth marble. There are thus $\binom{10}{1}$ ways of choosing one marble out of the remaining ten (because we dont care which color that last marble is). Therefore, the total number of possible combinations of four marbles where at least three are red is given above.

$\binom{4}{1}\cdot \binom{51}{1}=4\cdot 51=204$

There are $52$ cards in a standard playing card deck. Furthermore, there are 4 aces in the deck: ace of hearts, spades, diamonds, and clubs.

We first need to determine the number of ways we can draw an ace. Since there are four aces in the deck, there are four ways of drawing one ace, hence the $\binom{4}{1}$. Then, for each possible choice of drawing an ace, there are are 51 cards left in the deck after an ace has been drawn. So, there are $\binom{51}{1}$ ways of choosing the second card when the first was an ace. This gives us the final answer.

$\binom{4}{2}\cdot \binom{50}{4}=1381800$

There are $52$ cards in a standard playing card deck. Furthermore, there are 4 aces in the deck: ace of hearts, spades, diamonds, and clubs.

There are $\binom{4}{2}$ ways of choosing two aces from the usual four. After those have been drawn, there are $50$ remaining cards from which we must draw an additional $4$ cards. There are $\binom{50}{4}$ ways of doing this. So, for each of the $\binom{4}{2}$ ways we can draw $2$ aces, there are $\binom{50}{4}$ ways of drawing the other four cards. Therefore, the total number of ways of selecting a hand of six consisting of at least two aces is the answer you see above.

$\binom{4}{2}\cdot \binom{48}{4}=11467480$

There are $\binom{4}{2}$ ways one can select two aces from $4$ possible choices in the deck. Then, since we want exactly two aces in our hand, when picking our remaining four cards, we want to select from the set of all cards that does NOT have any aces. There are $48$ such cards (the usual 52 cards minus the 4 aces). The number of ways we can select $4$ cards from a deck with no aces is $\binom{48}{4}$. So, for each of the $\binom{4}{2}$ pairs of aces I pick, there are $\binom{48}{4}$ choices for the remaining four cards. Hence the final answer.

Previous Lesson

Back to Course

Next Lesson

Discrete Mathematics

Combinations

Combinations

Number of Ways of Selecting \(m\) Objects from a Set of \(n\)

What to Watch For

Why the Formula Works

Observation