$Project Greater Ed Logo$

Guessing Closed Formulas for Recursively Defined Sequences

Discrete Mathematics Guessing Closed Formulas for Recursively Defined Sequences

Why One Might Want a Closed Formula Instead of a Recurrence Relation

Recall…

A closed formula for a sequence $\{a_n\}_{n=1}^\infty$ is a rule/function $f:\mathbb{N}\rightarrow \mathbb{R}$ that assigns $a_n$ a value based on the value of $n$ . That is, $a_n=f(n)$ for all $n\geq 1$ .

In other words, a closed formula for a sequence is a rule that (almost) immediately tells you what each sequence element is (based on the location/index $n$ ).

Suppose we have a sequence $\{a_n\}_{n=1}^\infty$ defined recursively with initial conditions $a_1=1$ , $a_2=1$ , and recurrence relation $a_n=a_{n-1}+a_{n-2}$ . Suppose also that someone asked you to find the value of $a_{2351}$ . In order to do that, based on the rule given, we need to compute

$\begin{align}a_{2351}&=a_{2350}+a_{2349}\\&=(a_{2349}+a_{2348})+(a_{2348}+a_{2347})\\&=\ldots\end{align}$

And so on. In the above, we need to compute the previous sequence values to get the current one… but to do that we need to compute each of those previous values’ previous values, and so on. Not too much joy in that. Alternatively, one could generate the sequence out to the $2351$ st location… Sounds like a lot of work that nobody wants to do. So what can we do?

It would be nice if there was a closed formula that would tell us what the $2351$ st element of the sequence was. That would allow us to compute $a_{2351}$ without needing to compute all of the elements of the sequence that came before the $2351$ st one.

In the Fibonacci Sequence given above, the closed formula is given by

$\begin{align}a_n&=\frac{1}{\sqrt{5}}\left[\left(\frac{1+\sqrt{5}}{2}\right)^{n+1}-\left(\frac{1-\sqrt{5}}{2}\right)^{n+1}\right].\end{align}$

Still not pretty, but a lot more convenient if you want to compute the $2351$ st element of the Fibonacci Sequence, $a_{2351}$ . Just plug in $n=2351$ into the formula and hope that your calculator can handle the result!

$\begin{align}a_{2351}&=\frac{1}{\sqrt{5}}\left[\left(\frac{1+\sqrt{5}}{2}\right)^{2351+1}-\left(\frac{1-\sqrt{5}}{2}\right)^{2351+1}\right]\\&=9.5599853231642818235778509… \cdot 10^{490}\end{align}$

which is a lot more than the number of atoms estimated to be in the observable universe.

Guessing Closed Formulas from Recursively Defined Sequences

The Iteration Method

If given a recursive definition for a sequence $\{a_n\}_{n=1}^\infty$ , first write out the full computation of the first several elements of the sequence, continuing to do so until you see a pattern developing. Then, guess the rule based on that pattern.

Certainly, the above method is far from scientific, but it does help your pattern recognition skills to do things this way.

Using the Iteration Method to Find Closed Formulas for Recursively Defined Arithmetic Sequences

Essentially, we just compute $a_1$ , $a_2$ , $a_3$ , etc. showing all work, in hope that we will see a pattern allowing us to find a closed formula.

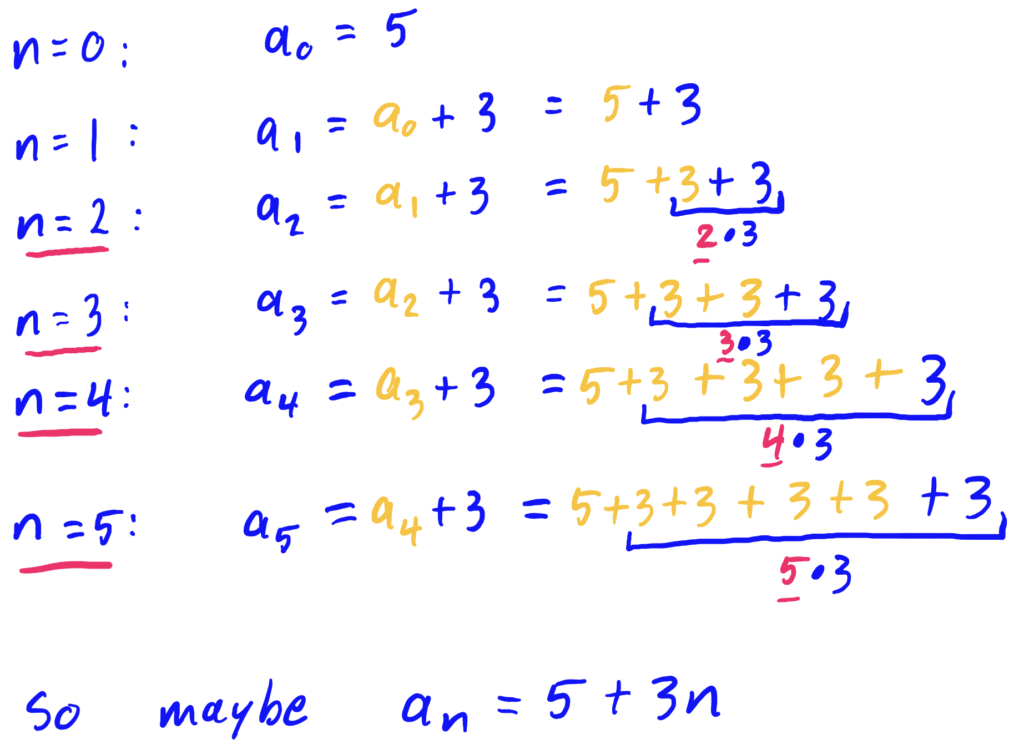
So, in the above, we computed everything but the final answer number for each of $a_1$ , $a_2$ , $a_3$ , etc. We noticed that there was a pattern developing on the right-hand-side of the equation, namely that if we were trying to compute, say $a_3$ , we noticed that we had $5$ plus 3 $3$ ’s being added together. Similarly for $a_4$ or $a_5$ , where we had $5$ plus 4 or 5 (respectively) $3$ ’s being added together. So, assuming that this pattern persists, for $a_n$ , no matter what $n$ is, we will probably have $5$ plus $n$ $3$ ’s added together. Thus, we can guess the formula

$\begin{align}a_n&=5+3n\end{align}$

**Notice that we don’t compute the final value of each $a_i$ (like computing $a_1=8$ for $n=1$ , $a_2=11$ for $n=2$ , etc.). Doing so would not help us see a pattern develop within the computations. So, it is usually best just to write things out to a point where you have a bunch of numbers added, subtracted, multiplied, etc. like what we have on the right-hand-side of each of the above equations.

Note that the above approach used to go from recursive definition to a closed formula is not something special that only works for recursively defined arithmetic sequences. It can be used for a litany of different types of sequences. Next, we show how to use this iterative method to find a closed formula for recursively defined geometric sequences.

Using the Iteration Method to Find Closed Formulas for Recursively Defined Geometric Sequences

As before, we write out the first several entries of the sequence and see if we can notice a pattern in how the entries are computed.

So, in the above, we computed everything but the final answer number for each of $a_1$ , $a_2$ , $a_3$ , etc. We noticed that there was a pattern developing on the right-hand-side of the equation, namely that if we were trying to compute, say $a_3$ , we noticed that we had $3$ times 3 $2$ ’s being added together. Similarly for $a_4$ or $a_5$ , where we had $3$ times 4 or 5 (respectively) $2$ ’s being multiplied together. So, assuming that this pattern persists, for $a_n$ , no matter what $n$ is, we will probably have $3$ times $n$ $2$ ’s multiplied together. Thus, we can guess the formula

$\begin{align}a_n&=3\cdot 2^n\end{align}$

Again, on the right-hand-side of each of the equations above, we did not compute the final value for each of $a_1$ , $a_2$ , $a_3$ , etc. We ended each line with a product of numbers to help us see the pattern from line to line. That is what allows us to determine a closed formula for the sequence.

Note!

The iteration method for guessing a closed formula for a recursively defined sequence is not limited to geometric or arithmetic sequences. You can use the same approach for a wide assortment of sequence types. However, not every sequence has a pattern than can be easily guessed. The Fibonacci formula given earlier is an example of such.

ALSO! Throughout this lesson, we’ve been GUESSING closed formulas for recursively defined sequences. Just because you see a pattern doesn’t necessarily make it the correct pattern! In the next lesson, we demonstrate how to mathematically prove that your guess is correct.