$Project Greater Ed Logo$

Functions and Their Representations

Discrete Mathematics Functions Basics Functions and Their Representations

One way we often relate one set to another in mathematics is by what is known as a function, which is a relation with a certain special property.

(Single-Variable) Function

A (single-variable) function from a set $A$ to a set $B$ is a machine, rule, method, diagram, graph, etc. that takes each element from $A$ as input and maps it to exactly one output element of $B$.

To be more precise, a function $f$ from set $A$ to set $B$ is a binary relation from $A$ to $B$ so that each element of $A$ is related to exactly one element of $B$.

It is helpful to think of a function as a process or a machine that takes in some input, does something to it, and then spits out some output. See image below.

$x$ in the above diagram is called an input or argument of the function
$f$ is the function’s name
$f(x)$ is the output of function $f$ on input $x$

Note on Notation

When labeling/naming a function, we usually use the letters $f$, $g$, or $h$, but there is technically no restriction on what you can call a function. If you see expressions like $“f(x)”$, note that $f(x)$ is NOT TECHNICALLY REFERRING TO A FUNCTION. It is referring to the OUTPUT of the function $f$ on some input $x$. The function itself is called $f$.

Evaluating Outputs Using Different Function Representations

Let the function $f$ be a function from $A$ to $B$ as defined using the diagram below. Is $f$ a function? If so, use the diagram to find $f(1)$ and $f(3)$.

Yes, $f$ is a function. Note that each element in the left potato maps to exactly one element in the right potato. If there were multiple arrows coming out of one element in the left potato, then $f$ would not be a function (because it assigns an input to more than one output).

$f(1)=3$, follow the arrow from input $1$ in the left potato to output $3$ in the right potato

$f(3)=1$, again, following the arrow from the argument $3$ in the left potato to the output $1$ in the right potato.

Let $f=\{(1,2),(3,1),(5,3),(0,7),(2,1)\}$. Is $f$ a function? If so, use it to find $f(5)$ and $f(0)$.

Answers:

Yes, $f$ is a function. Each input ($x$-value in each ordered pair) goes to a single output ($y$-value); i.e. no input goes to two different outputs. $f$ would not be a function if we had, say $(1,2)$ and $(1,3)$ in the set, because this would indicate that $1$ is mapped to two different outputs.

$f(5)=3$

$f(0)=7$

**Note that we could have just as easily defined $f$ using a table rather than a list of input-output pairs (see below). The problem works essentially the same way.

Inputs ($x$-values)	Outputs ($y$-values)
1	2
3	1
5	3
0	7
2	1

Let $f$ be a function defined by the output of $f$ on $x$: $f(x)=x^2-2x+1$. Find $f(1)$ and $f(0)$

$f(1)=(1)^2-2(1)+1=0$

$f(0)=(0)^2-2(0)+1=1$

The “rule” for the function, given by the formula $f(x)=x^2-2x+1$, tells us how to find the output of $f$ given any input $x$ value we wish to input. To use this algebraic rule, simply replace the $x$’s you see with the desired input value, then simplify the result algebraically.

**Note that simple algebraic rules such as this one is always a function.

Let $f$ be defined by the graph shown below. Is $f$ a function? If so, determine the value of $f(0)$ and $f(-1)$.

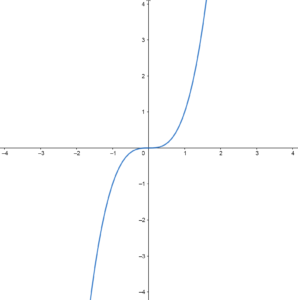
$f$ is indeed a function because each $x$-value goes to exactly one $y$-value. If $f$ were NOT a function, then you would be able to find a single $x$-value that gives you at least two different $y$-values.

$f(0)=0$. Along the $x$-axis, go to where $x=0$, then find the corresponding $y$-value.

$f(-1)=-1$. Go to $x=-1$ on the $x$-axis, then move straight down until you hit the graph. The $y$-value is the output of this function.

$f(1)=3$, $f(3)=1$, and $f(4)=7$

Remember that $f(x)$ means “what is the output of the function on input $x$” (where $x$ is a number). Follow the arrows from $1, 3$ and $4$, respectively, in the left potato to their corresponding output in the right potato.

$f(2)=4$, $f(5)=-1$, and $f(3)=0$.

Remember that $f(x)$ means “what is the output of the function on input $x$” (where $x$ is a number). Follow the arrows from $2, 5$ and $3$, respectively, in the left potato to their corresponding output in the right potato.

$\{1,3\}$.

This problem is asking the opposite question, compared to the last two problems. Here, we want to know all possible inputs that give a specific output. So, look for arrows pointing TO $5$, finding all the elements in the left potato (your possible inputs) that have arrows pointing from them to the number $5$. Put those inputs in curly brace set notation (because the problem asked for a set).

$x=$inputs	$y=f(x)$
1	5
2	3
3	6
4	-1
5	0

$f(1)=5$, $f(4)=-1$, and $f(2)=3$

The inputs are $1,\ 4,$ and $2$ respectively. Find these values in the left column, then write the corresponding output from the right column in the same row as the input.

$f(2)=4$ and $f(5)=2$.

The inputs given are $2$ and $5$. Find the ordered pair whose first entry is each of these and write the corresponding output, which is the second entry in the ordered pair corresponding to that input.

$f(2)=2^2-10=-6$ and $f(-2)=(-2)^2-10=-6$.

Every place you see an $x$ in the function rule, replace it with the given input (i.e. the number in parentheses next to the $f$.

$g(1)=3(1)^2-5(1)+1=0$ and $g(-3)=3(-3)^2-5\cdot (-3)+2=44$.

Every place you see an $x$ in the function rule, replace it with the given input (i.e. the number in parentheses next to the $g$.

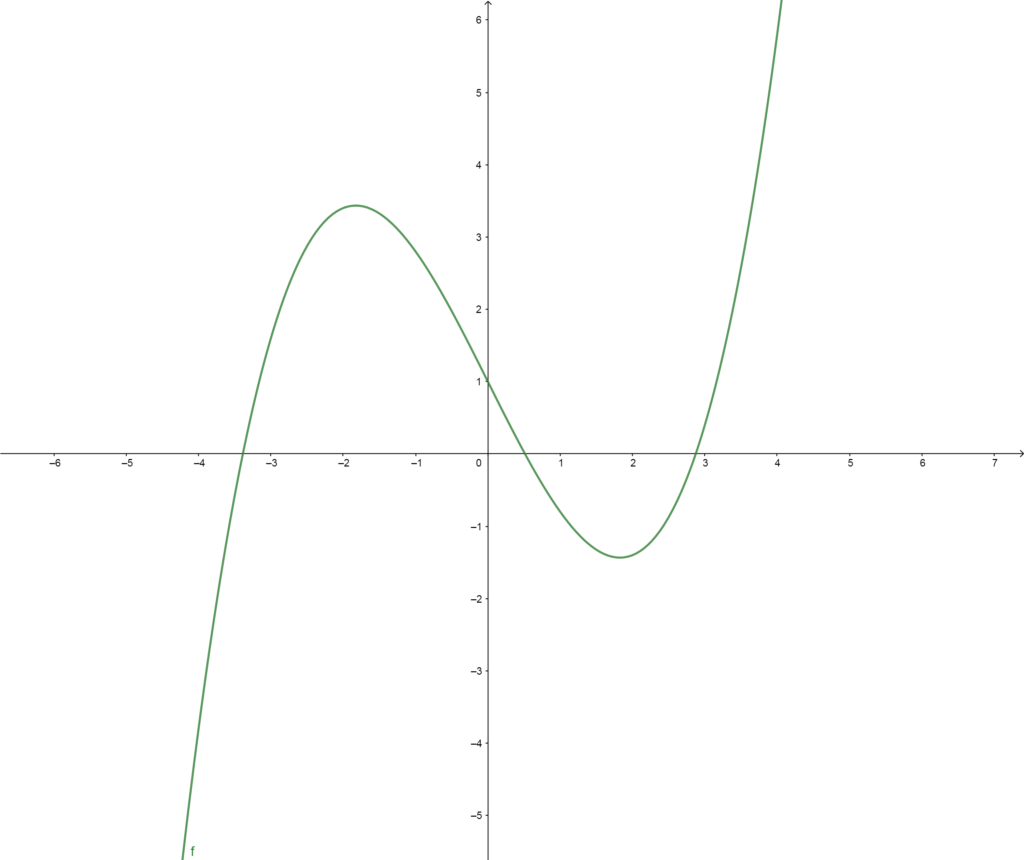
Solution: (Note these are estimates. Your answers might be slightly different)

$f(-1)=2.75$

$f(3)=0.5$

$f(4)=7$

Note that these answers are estimates and may differ a bit from your final answers

$g(-0.5)=0.83$

$g(1.20)=1.8$

$g(0.14)=0.95$

Previous Lesson

Back to Lesson

Next Topic

Inputs (\(x\)-values)	Outputs (\(y\)-values)
1	2
3	1
5	3
0	7
2	1

\(x=\)inputs	\(y=f(x)\)
1	5
2	3
3	6
4	-1
5	0