A Library of Commonly Used Functions (and Their Graphs)
The graph of any function defined on an interval can be obtained (roughly) by plugging in sufficiently many \(x\)-values into the function in order to get corresponding \(y\)-values, then connecting the dots on your graph.
Some functions, or variations of them, are ubiquitous in mathematics. It is beneficial, therefore, to know what their graphs look like in addition to some of their key features. We will refer to these commonly used functions as library functions. Their graphs are shown below. Commit these to memory as we will be transforming them (altering them to get new functions) in the next lesson.
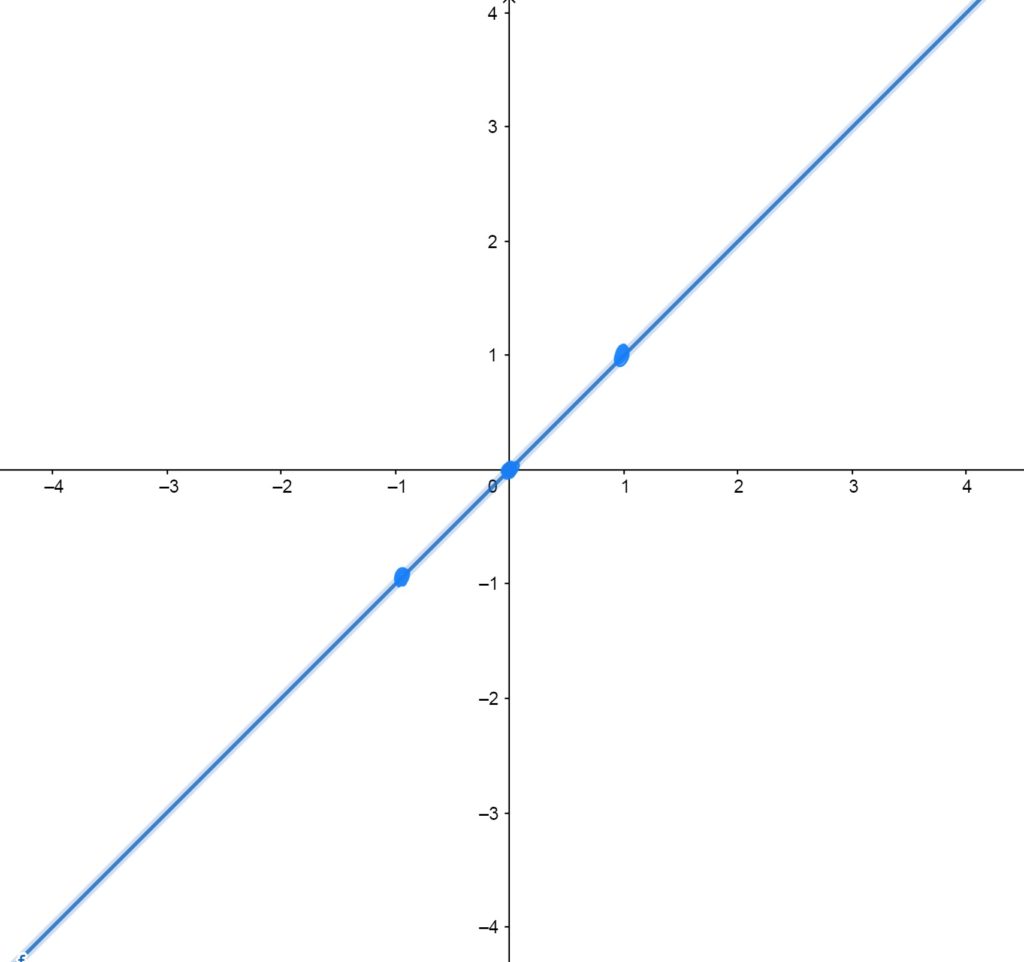
\(f(x)=x\)
Key Features:
Passes through the origin in a straight line. All linear functions can be obtained by shifting, reflecting, and/or scaling this function.
Control/Reference Points \(f(x)=x\) Passes Through
The graph of \(f(x)=x\) passes through \((0,0)\), \((1,1)\), and \((-1,-1)\).
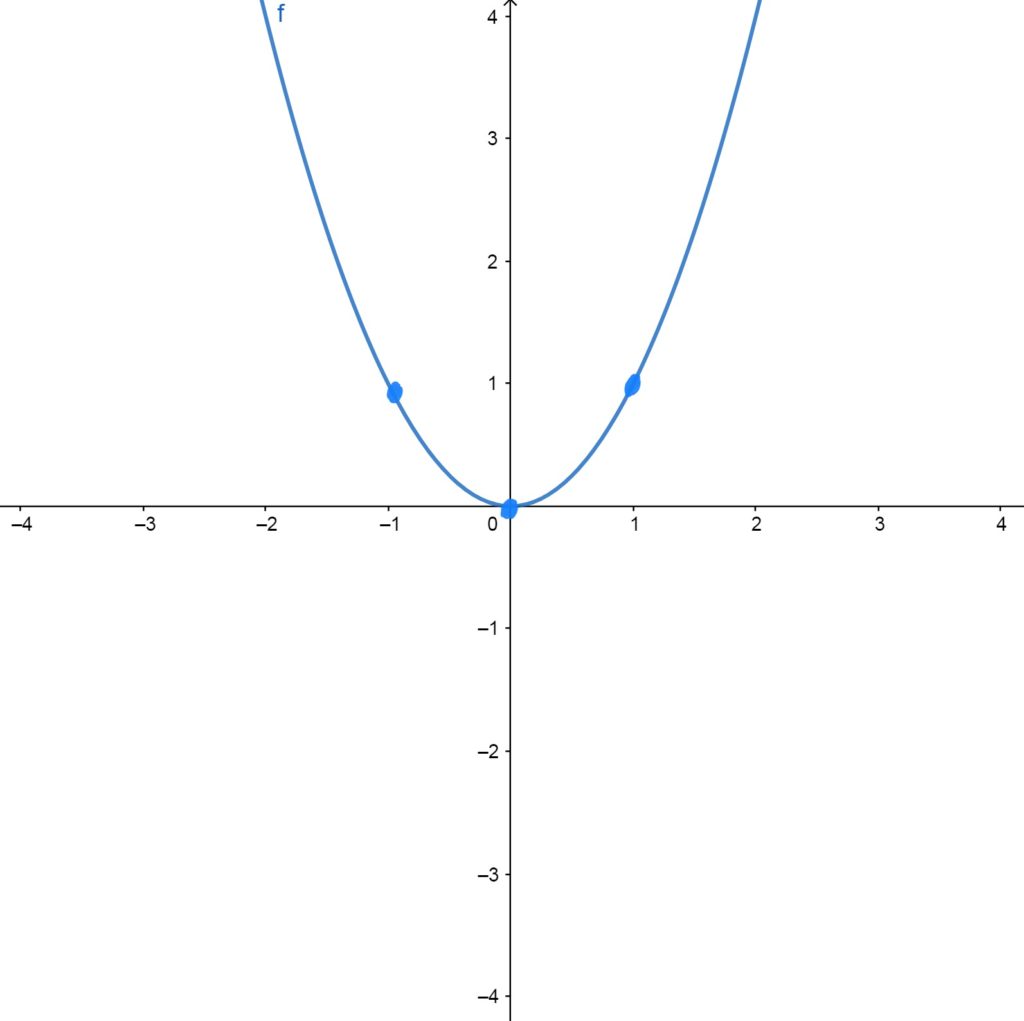
\(f(x)=x^2\)
Key Features:
Has vertex at the origin. All \(y\)-values are nonnegative (i.e. above the \(x\)-axis). The graph is symmetric about the \(y\)-axis (i.e. if you reflect it over the \(y\)-axis, you get what you started with).
Control/Reference Points \(f(x)=x^2\) Passes Through
The graph passes through the points \((-1,1)\), \((0,0)\), and \((1,1)\).
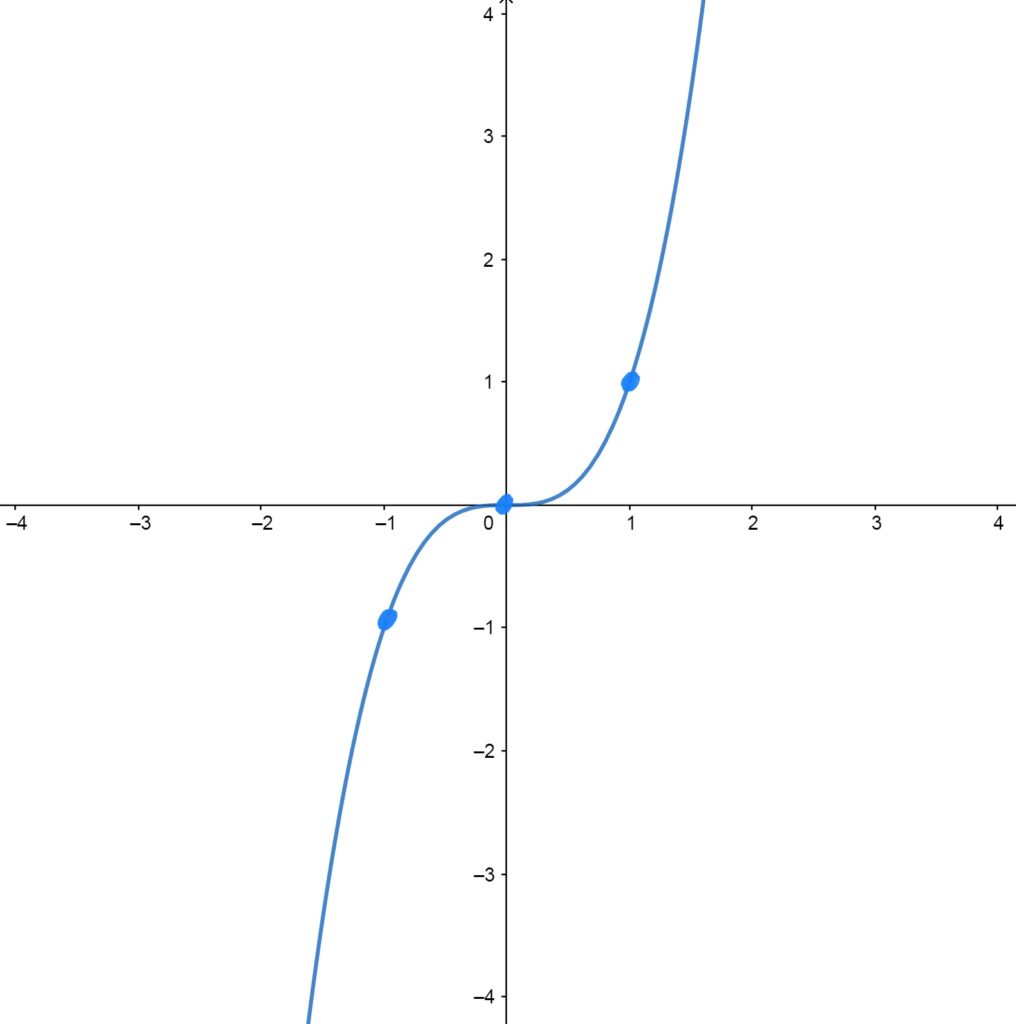
\(f(x)=x^3\)
Key Features:
Passes through the origin. Symmetric about the origin (i.e. if you flip it both over the \(y\)-axis and the \(x\)-axis, you get what you started with). The slope of the graph at \(x=0\) is \(0\). The function is defined everywhere, and hits every possible \(y\)-value.
Control/Reference Points \(f(x)=x^3\) Passes Through
The graph passes through \((-1,-1)\), \((0,0)\), and \((1,1)\).
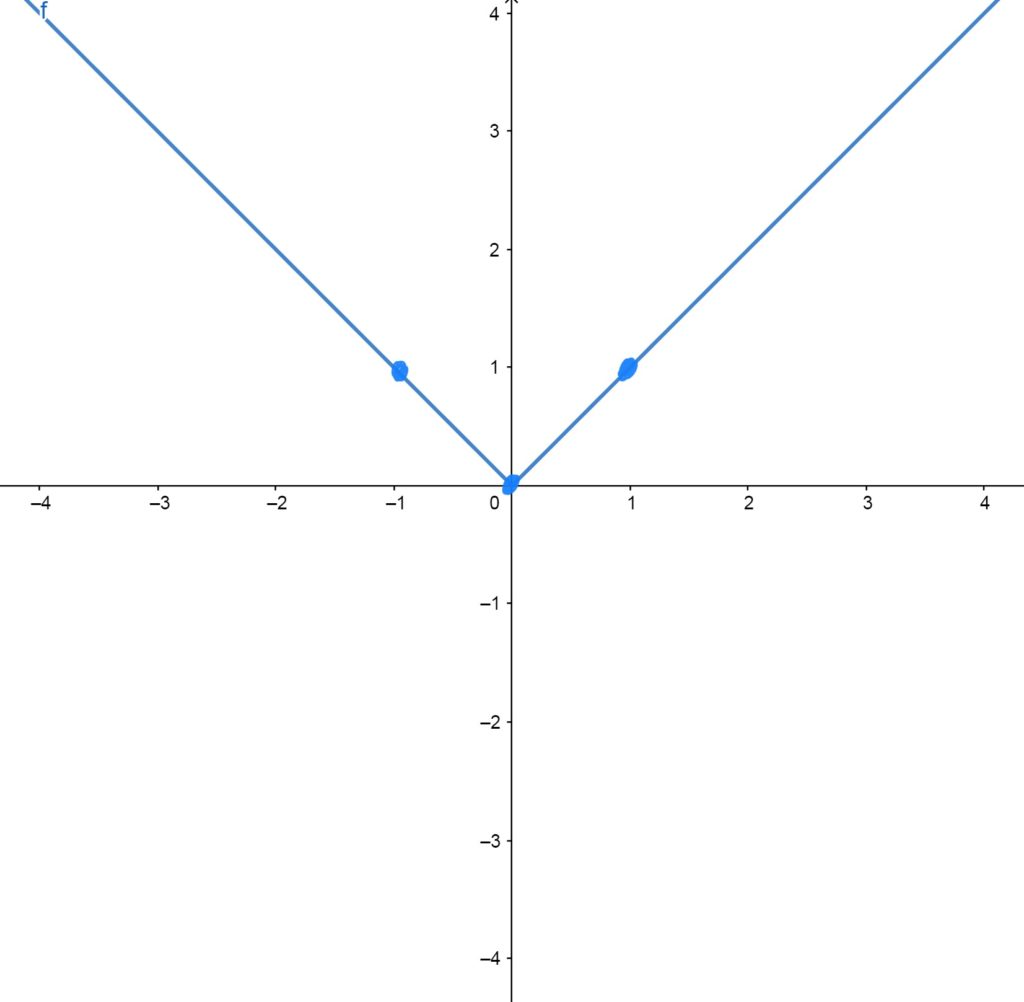
\(f(x)=|x|\)
Key Features:
Looks like the letter “v”. This graph is the same as \(f(x)=x\), except that the negative part of \(f(x)=x\) is “flipped up” to the positive side of the \(x\)-axis, so that the \(y\)-values are made positive (which reflects what absolute values do algebraically: make the stuff on the inside positive). As such, \(|x|\) cannot produce a negative \(y\)-value output.
Control/Reference Points \(f(x)=|x|\) Passes Through
The graph passes through the points \((-1,1)\), \((0,0)\), \((1,1)\).

\(f(x)=\sqrt{x}\)
Key Features:
Has undefined slope at the origin. Is the same as the graph of \(x^2\), except flipped on it’s side, and broken in half. \(sqrt{x}\) has no negative \(y\)-values because there is no number with a negative square root. Further, \(sqrt{x}\) is not defined for \(x<0\) because you cannot plug negative numbers into \(sqrt{x}\)… unless of course you like imaginary numbers.
Control/Reference Points \(f(x)=\sqrt{x}\) Passes Through
The graph passes through the points \((0,0)\) and \((1,1)\).
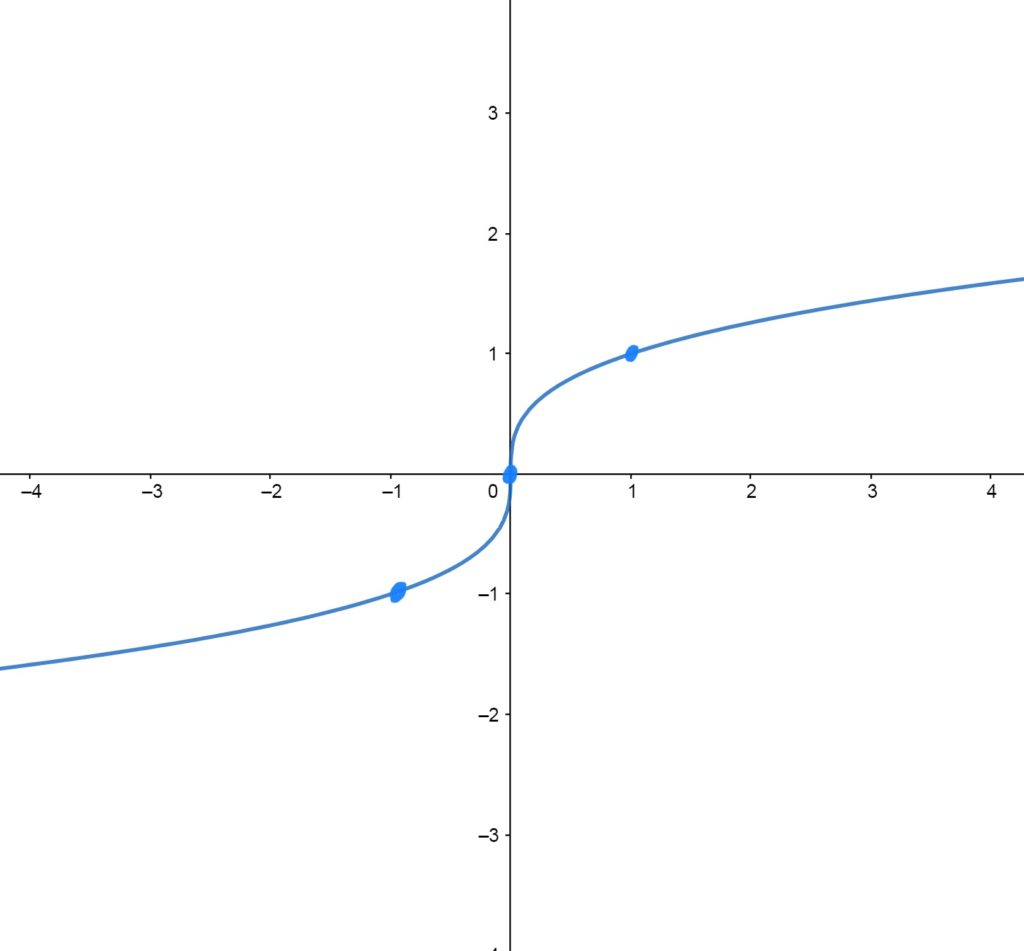
\(f(x)=\sqrt[3]{x}\)
Key Features:
This graph is the same as \(x^3\), except reflected through the diagonal line \(y=x\); In a weird way, you can think of \(\sqrt[3]{x}\) as the “sideways” or “horizontal” version of \(x^3\). \(sqrt[3]{x}\) has undefined slope at the origin. The graph goes up and to the right forever; as high as you like. The graph also goes down and to the left as low as you like. The function is defined everywhere, and hits every possible \(y\)-value.
Control/Reference Points \(f(x)=\sqrt[3]{x}\) Passes Through
The graph passes through the points \((-1,-1)\), \((0,0)\), and \((1,1)\).
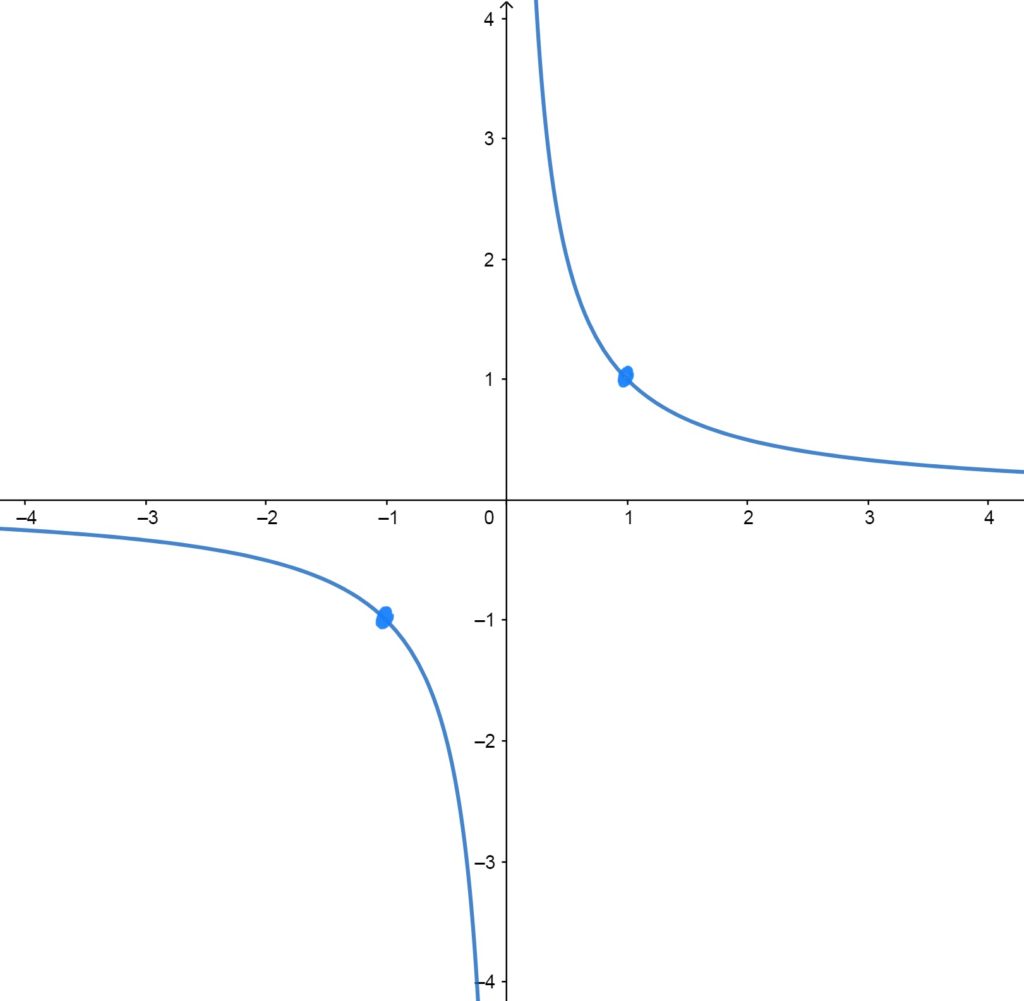
\(f(x)=\frac{1}{x}\)
Key Features:
Symmetric about the lines \(y=x\) and \(y=-x\); meaning, the positive part looks like the negative part, just flipped. The graph cannot have a \(y\)-value of \(0\), nor is the function defined at \(x=0\).
Control/Reference Points \(f(x)=\frac{1}{x}\) Passes Through
The graph passes through the points \((-1,-1)\), \((1,1)\).
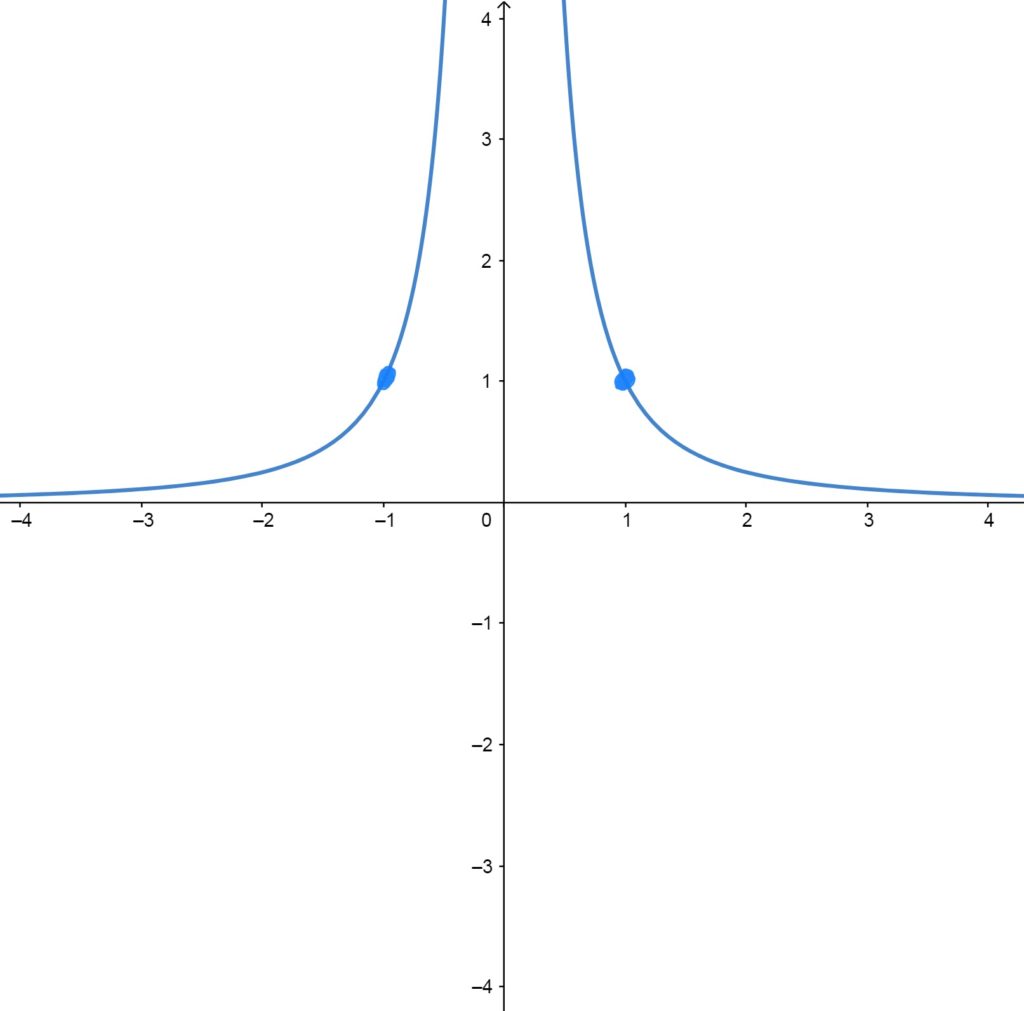
\(f(x)=\frac{1}{x^2}\)
Key Features:
Symmetric about the \(y\)-axis. The function is not defined at \(x=0\) and cannot ever have a zero or negative \(y\)-value (i.e. the graph never touches the \(x\)-axis or crosses below it).
Control/Reference Points \(f(x)=\frac{1}{x^2}\) Passes Through
The graph passes through \((-1,1)\) and \((1,1)\).
