Function Transformations: Shifting, Scaling, Reflecting
One can transform simple functions, such as our library functions, to obtain a wide variety of more complicated functions. The following list describes each transformation and explains the effect the transformation has on the shape (or position) of the graph of the original function.
Shifting Vertically
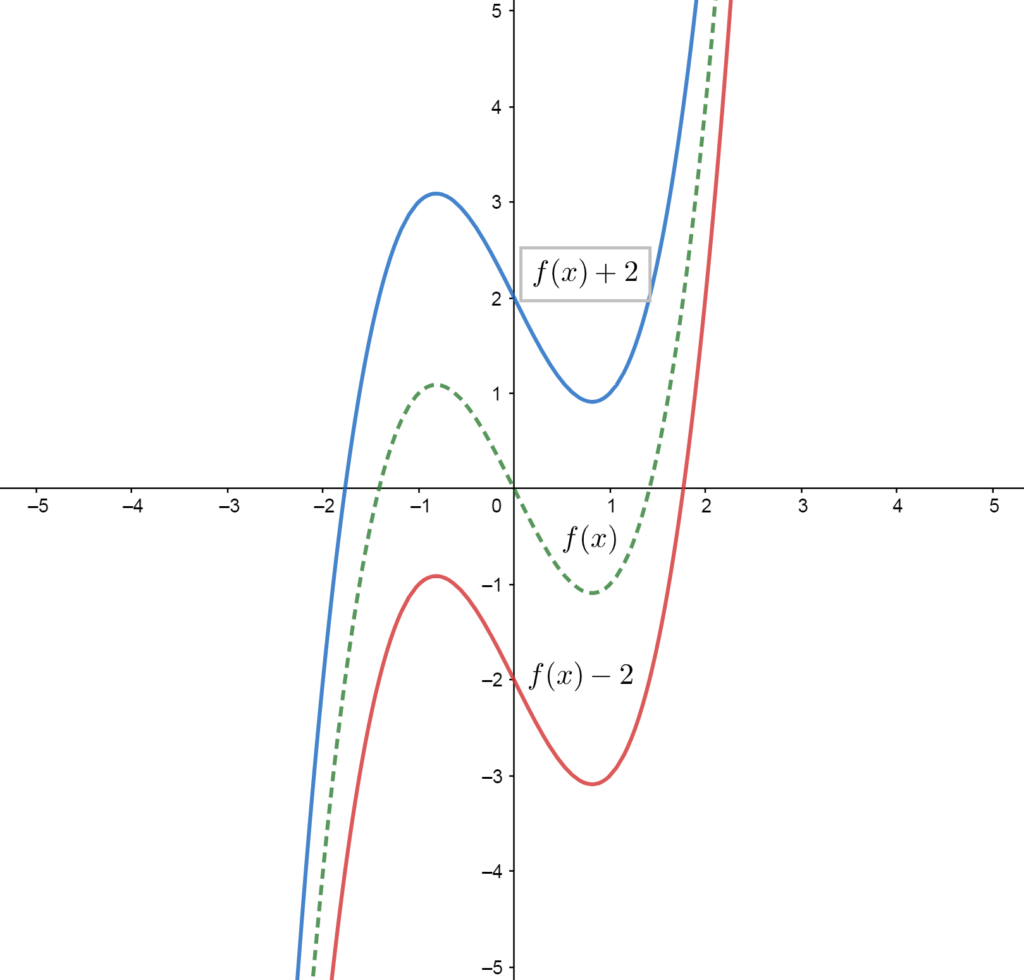
A function \(f\) can be shifted (or translated) vertically by adding or subtracting a number from the entire function. Adding a number shifts the function upward (because you are adding to the \(y\)-values that come out of \(f\)). Subtracting a number shifts the function downward (because you are taking away from the \(y\)-values that come out of \(f\)).
- \(f(x)+k\) shifts \(f\) up by \(k\).
- \(f(x)-k\) shifts \(f\) down by \(k\)
Shifting Horizontally
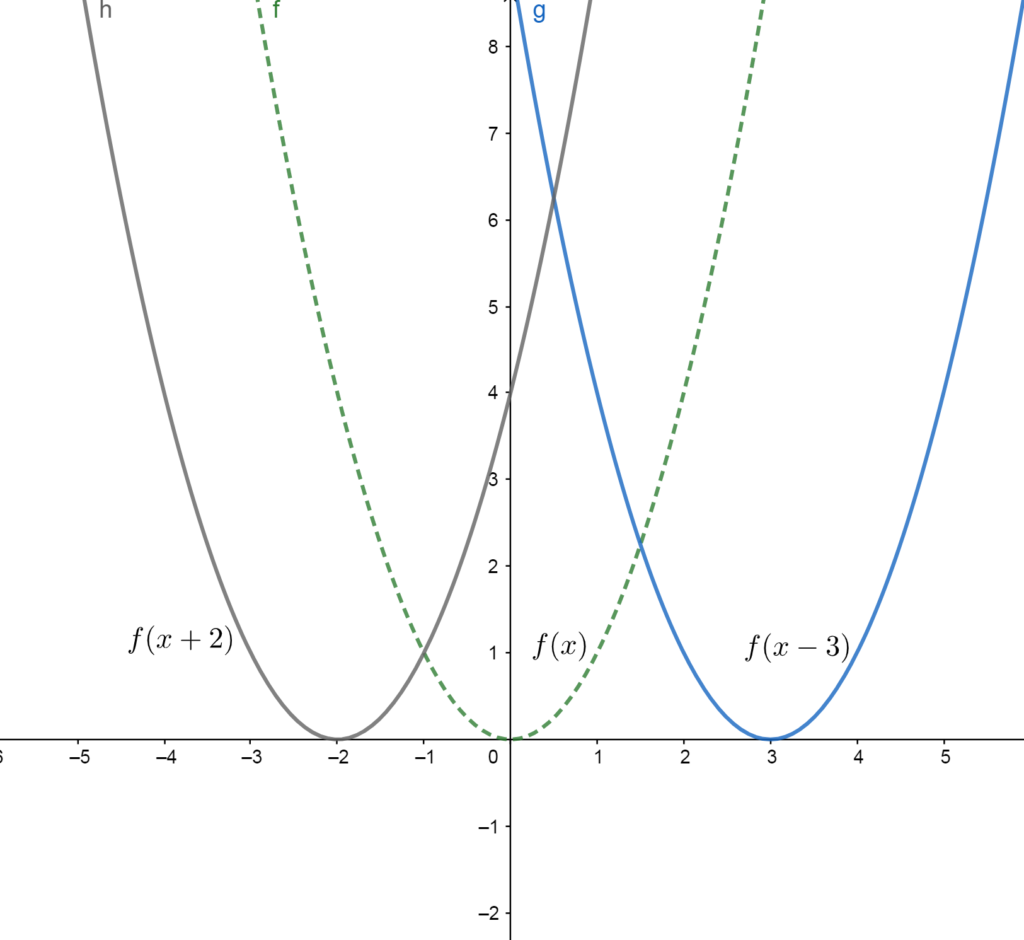
A function \(f\) can be shifted horizontally by adding or subtracting a constant from the input \(x\).
Adding a number to the input \(x\) can be thought of as “making the graph start earlier.” Subtracting a number from the input \(x\) can be thought of as “making the graph start later.”
- \(f(x+k)\) shifts \(f\) to the left by \(k\)
- \(f(x-k)\) shifts \(f\) to the right by \(k\)
Reflecting Vertically (over the \(x\)-axis)
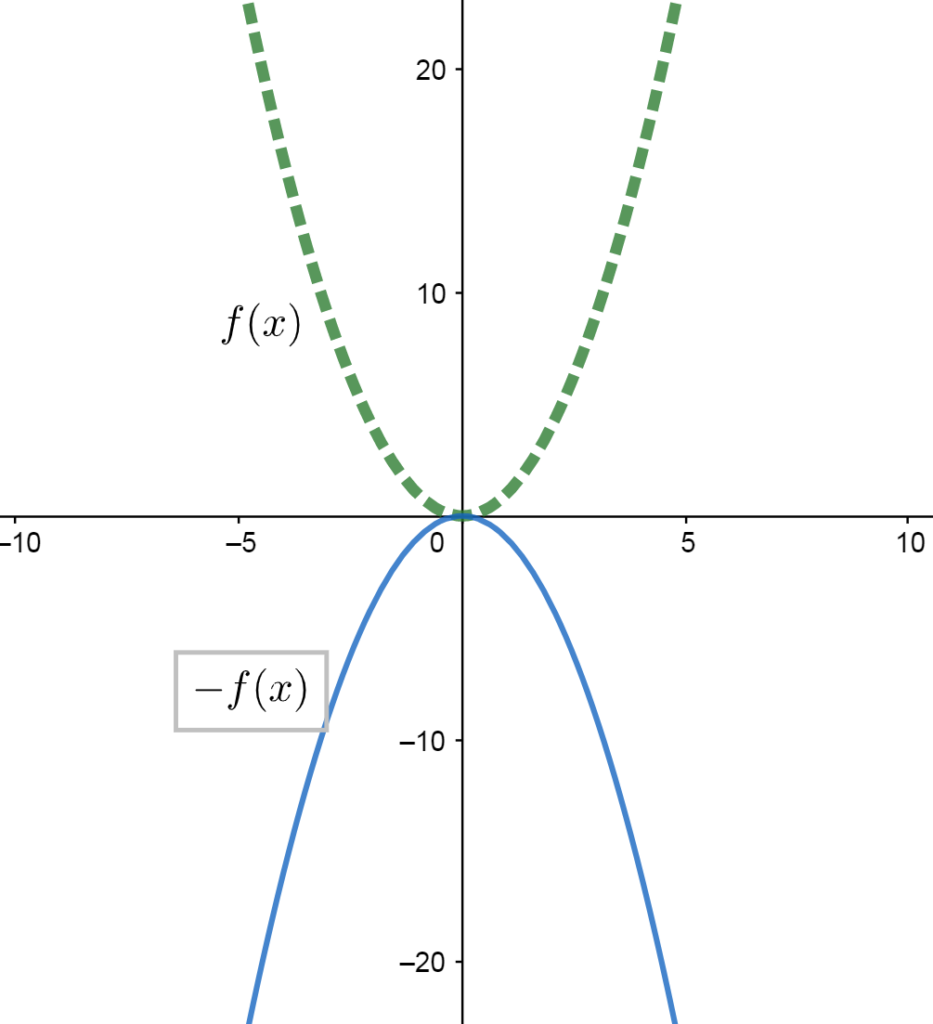
A function \(f\) can be reflected/flipped over the \(x\)-axis simply by multiplying \(f\) by a negative number (usually by -1).
Algebraically, this negative out in front has the effect of making every positive \(y\)-value output of \(f\) negative, and every negative output \(y\)-value positive.
- \(-f(x)\) reflects \(f\) over the \(x\)-axis
Horizontal Reflection (over the \(y\)-axis)
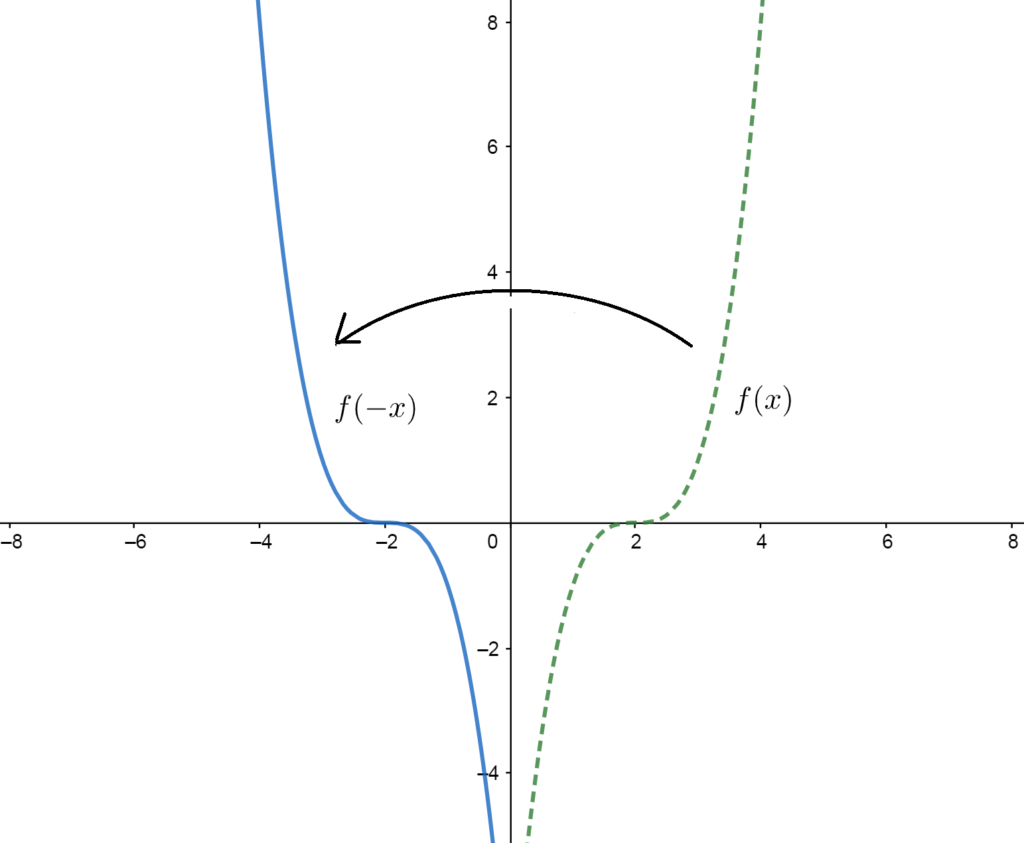
A function \(f\) can be reflected/flipped over the \(y\)-axis simply by multiplying the input \(x\) inside the function by a negative number.
This takes all positive inputs and makes them negative and all negative inputs and makes them positive, effectively flipping the graph horizontally.
- \(f(-x)\) reflects \(f\) across the \(y\)-axis.
Scaling Vertically
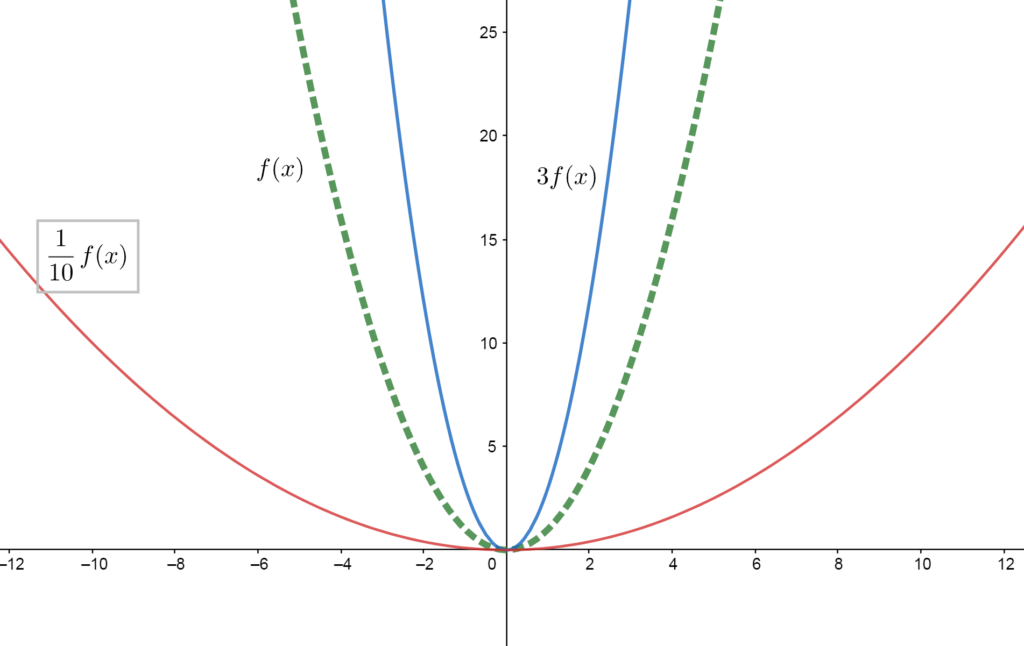
A function can be scaled vertically by multiplying the function by a constant.
The graph of function \(f\) will be stretched vertically if \(f\) is being multiplied by a number \(>1\). (See blue function compared to green at left)
The graph of \(f\) will be compressed vertically if \(f\) is being multiplied by a positive number \(<1\). (See red function compared to green at left)
Multiplying a function by a scalar number has the algebraic effect of amplifying the \(y\)-values that come out of the function, multiplying them by a certain amount, either making the function “quieter” or “louder” depending on the number.
Scaling Horizontally
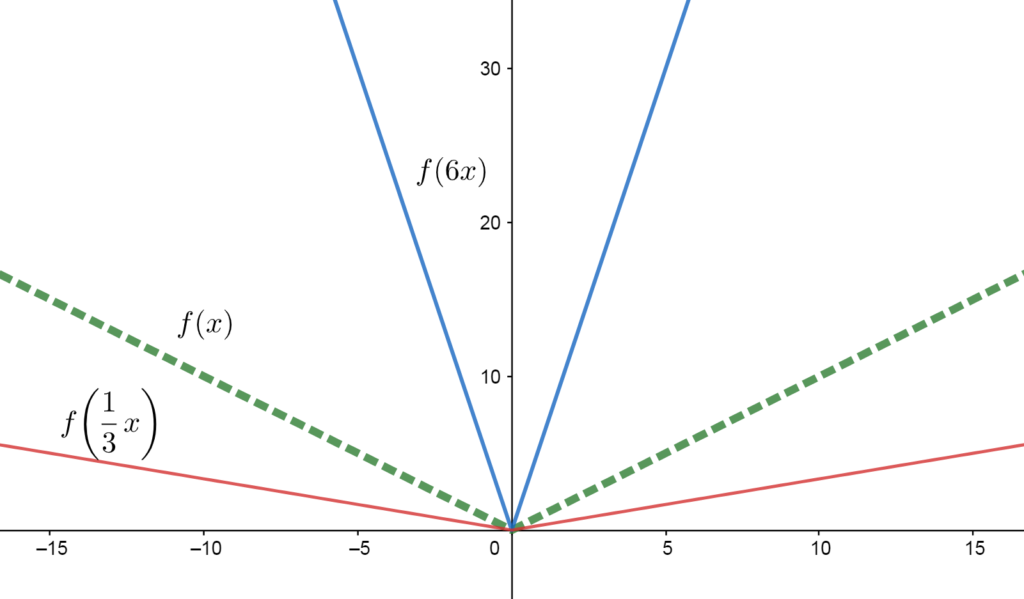
A function \(f\) can be scaled horizontally by multiplying the input \(x\)-values by a scalar prior to applying the rule for \(f\).
Multiplying \(x\) by a number greater than 1 has the effect of making inputs bigger, and thus compressing the graph horizontally. (see blue graph compared to green)
Multiplying \(x\) by a number less than 1 makes inputs smaller, effectively stretching out the graph horizontally. (See red graph compared to green)
Combining Transformations
A variety of transformations can be applied to any function to yield a new function. For instance, a given function such as \(f(x)=(x-3)^2+4\) is nothing more than \(x^2\) shifted to the right by 3 and then up by 4. To correctly identify what happens to the graph of a function after the transformations have been applied, it is best to use the following “Order of Operations”
- Determine if the function was shifted horizontally
- Determine if the function was reflected horizontally
- Determine if the function was scaled horizontally
- Determine if the function was reflected vertically
- Determine if the function was scaled vertically
- Determine if the function was shifted vertically
Library function: \(f(x)=x^2\)
Transformations:
- Shifted up (vertically) by 5
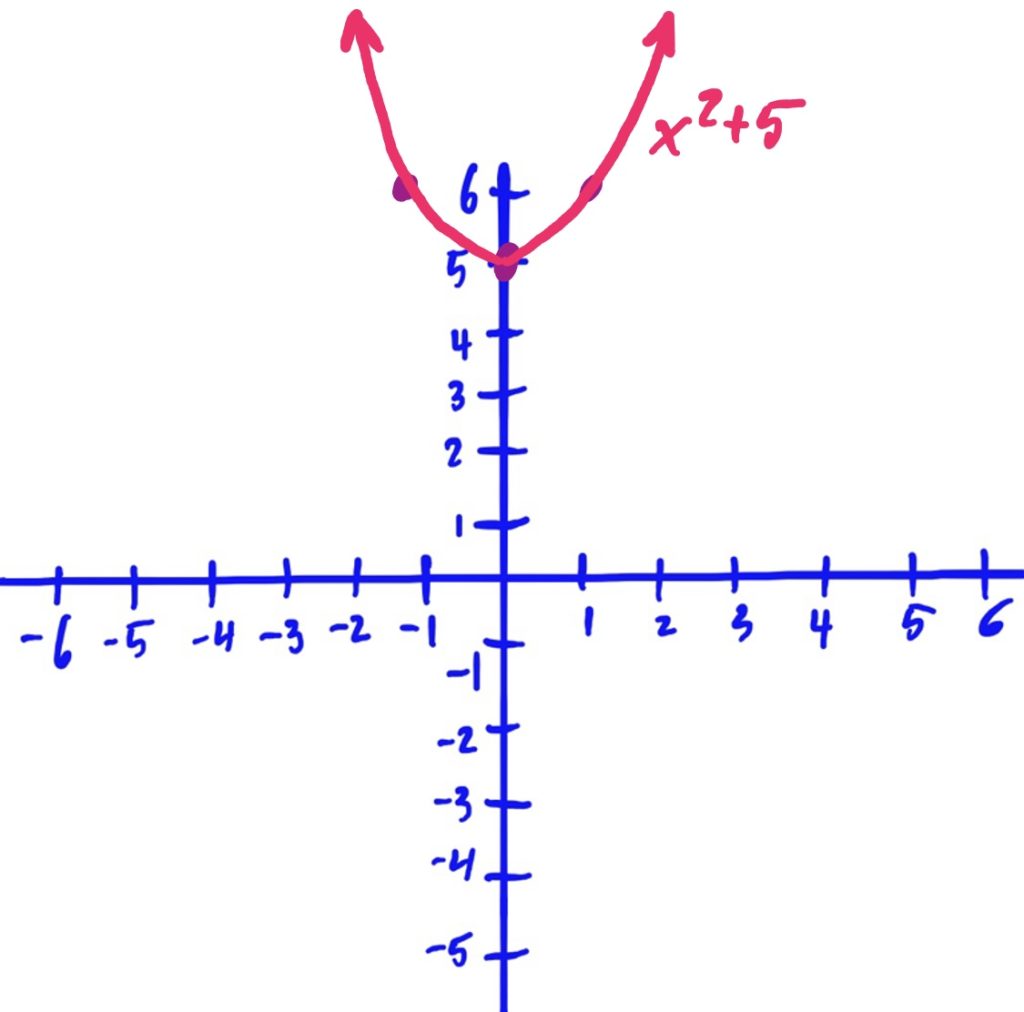
Solution:
Library function: \(f(x)=x^3\)
Transformations applied:
- Shifted down by 2
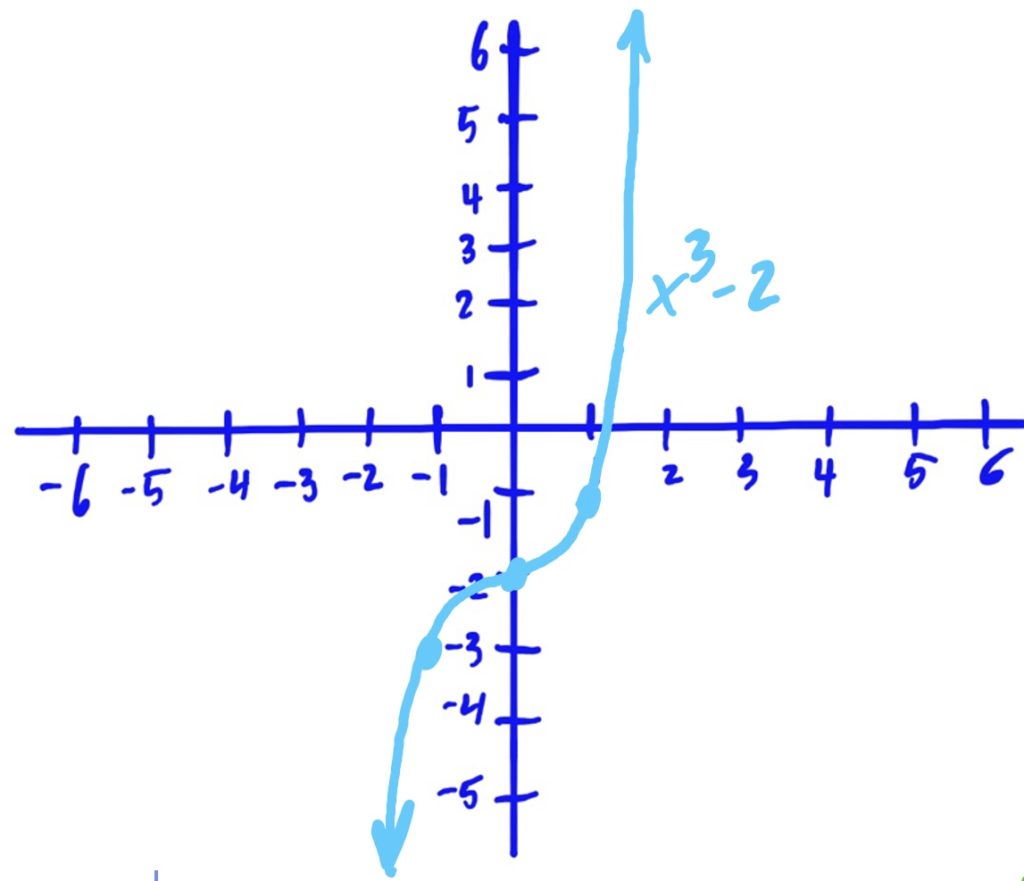
Solution:
Library Function: \(f(x)=|x|\)
Transformations:
- Shifted to the right by 2
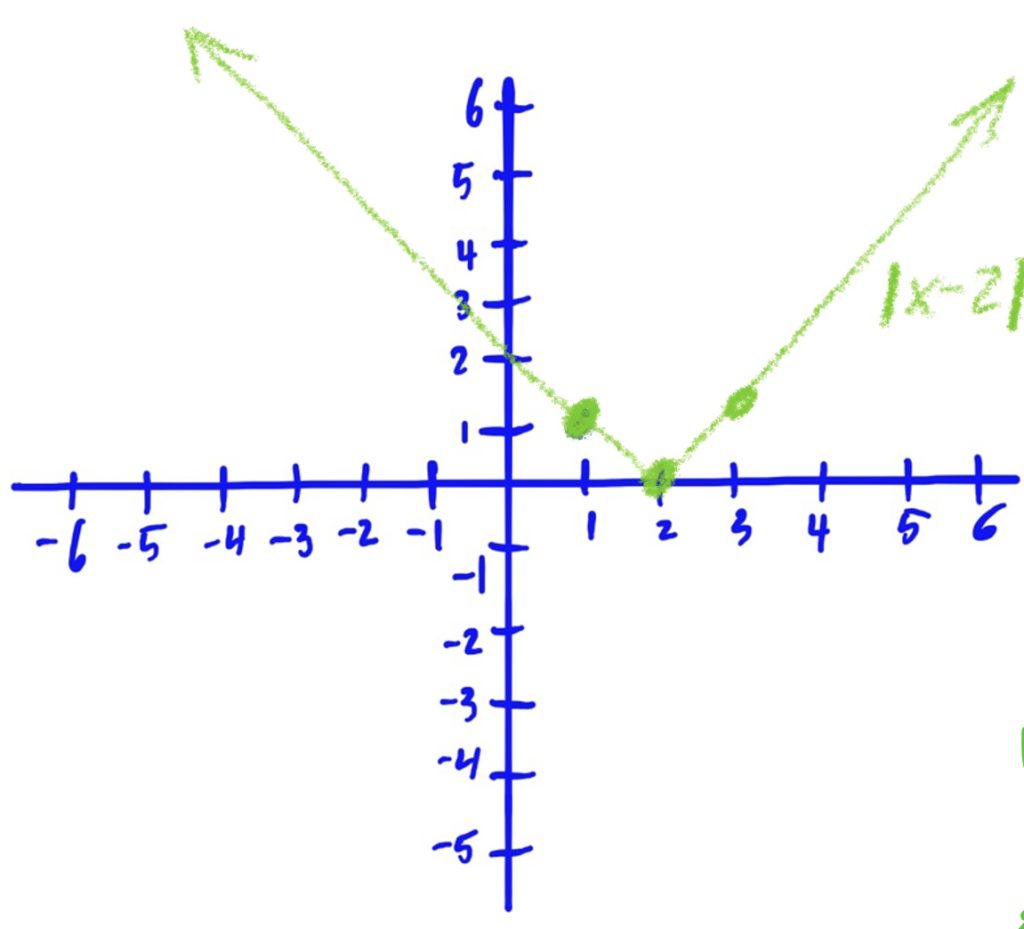
Library Function: \(f(x)=\frac{1}{x}\)
Transformations applied:
- shifted to the left by 5
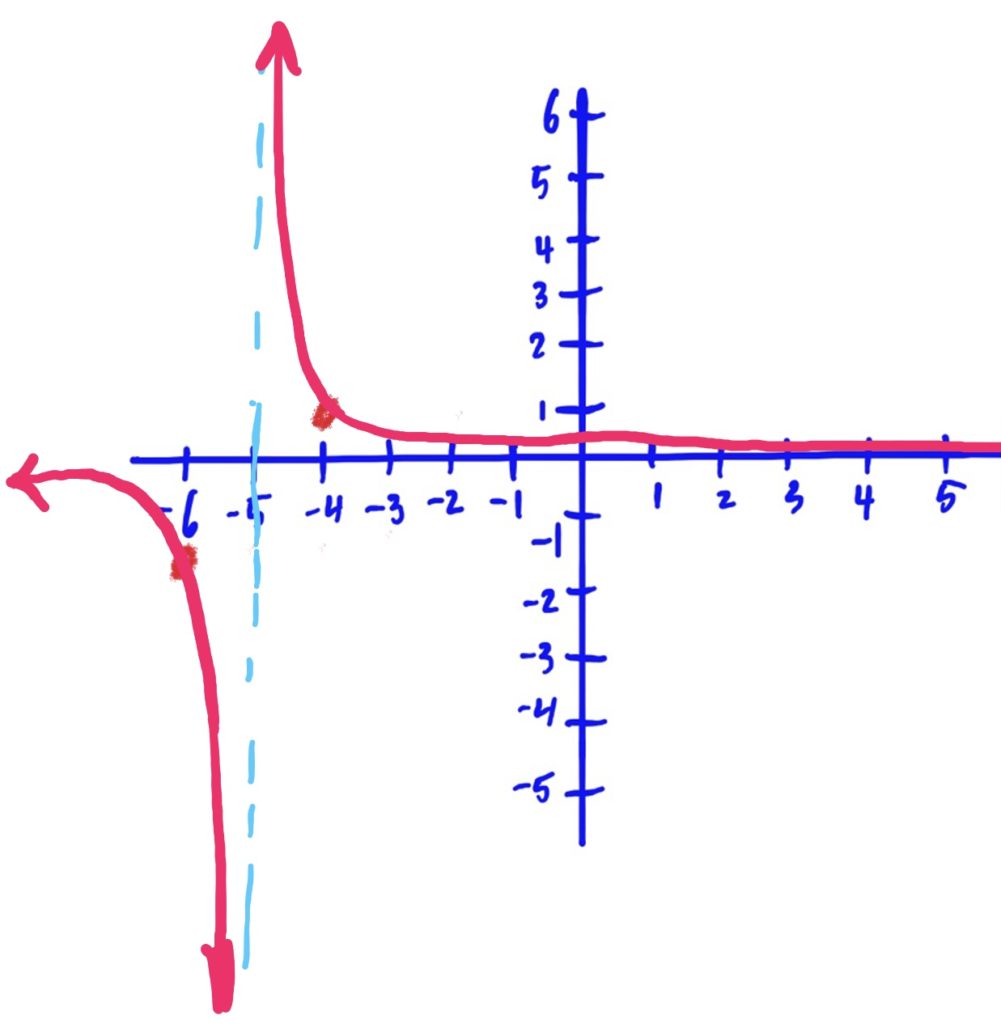
Library Function: \(f(x)=x\)
Transformations applied:
- Shifted to the right by 2, then
- Shifted up by 4
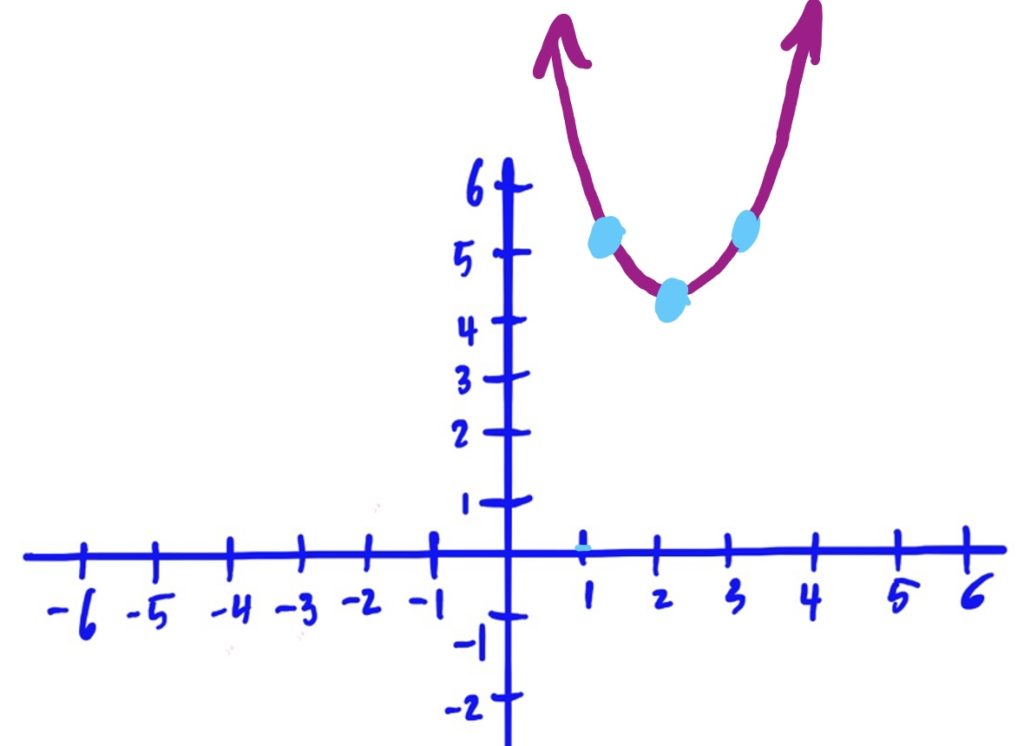
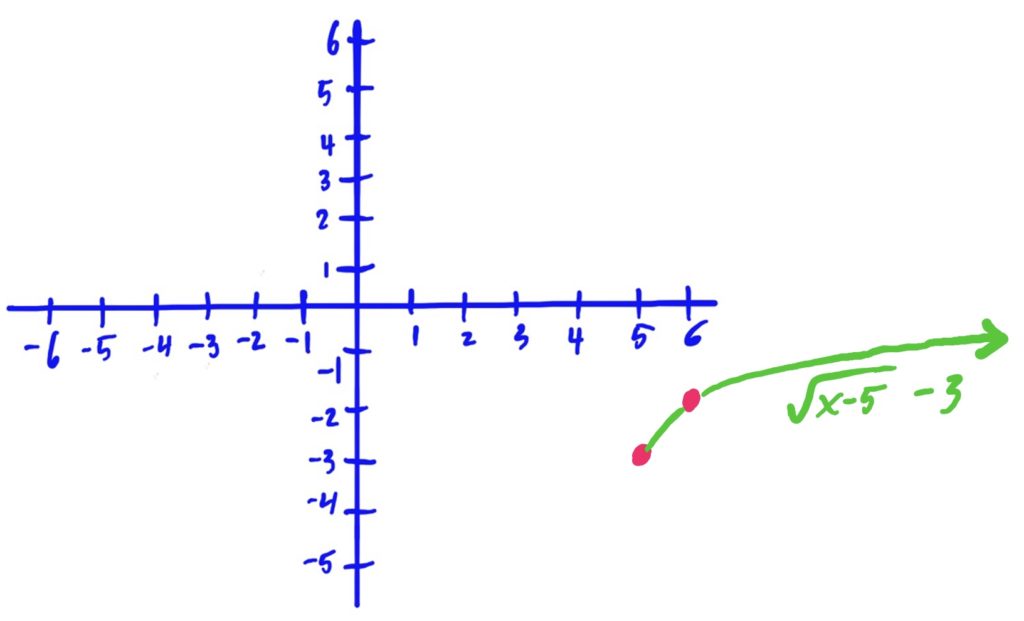
Library Function: \(f(x)=\sqrt{x}\)
Transformations applied:
- shifted to the right by 5, then
- shifted down by 3
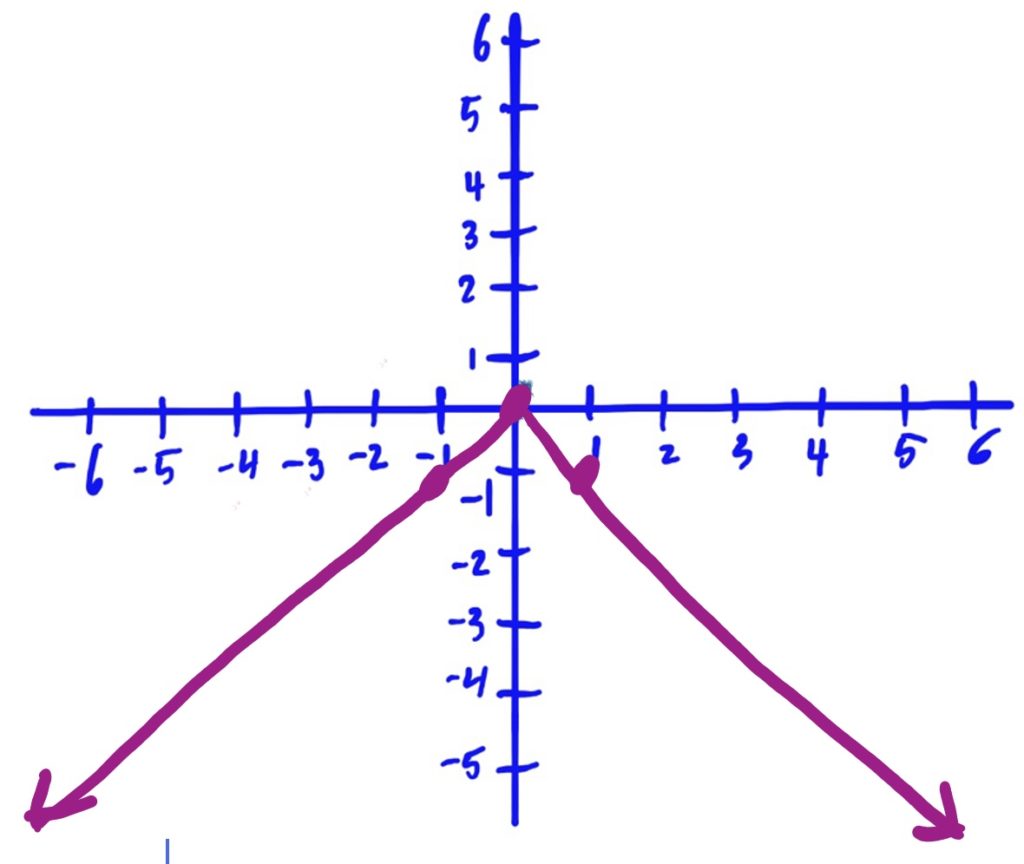
Library Function: \(f(x)=|x|\)
Transformations applied:
- Flipped over the \(x\)-axis (i.e. flipped vertically)
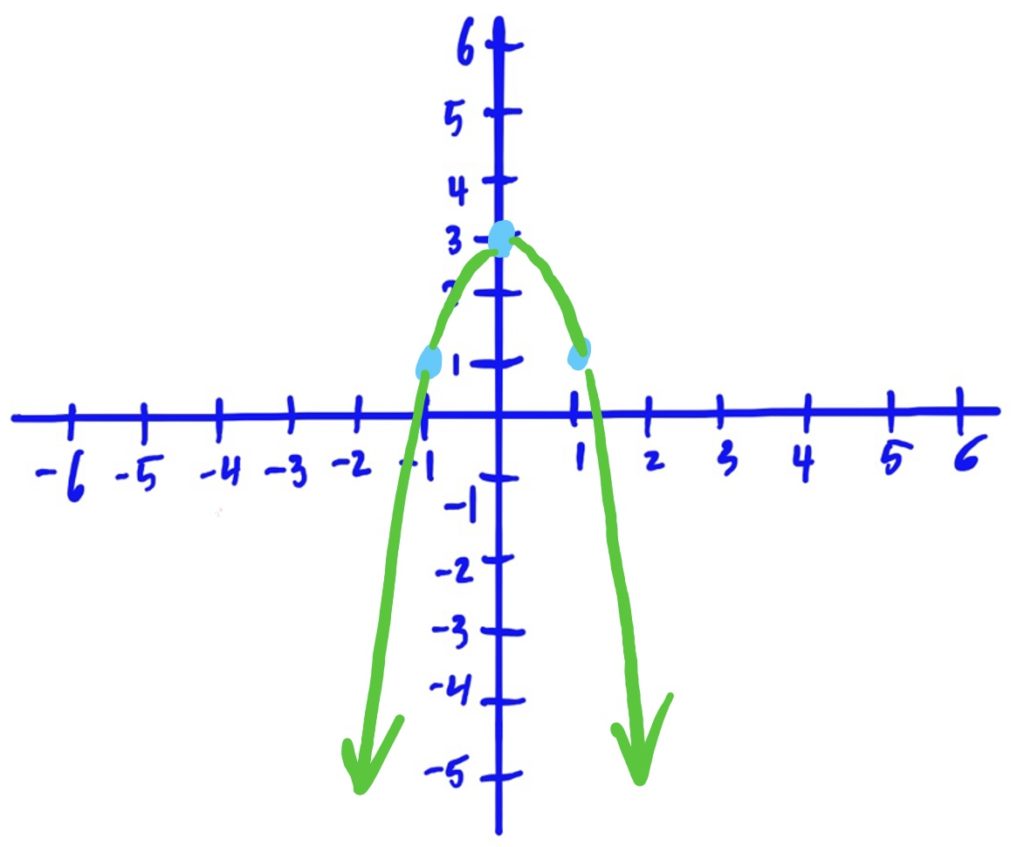
Library Function: \(f(x)=x^2\)
Transformations Applied:
- Reflected over the \(x\)-axis, then
- shifted up by 3
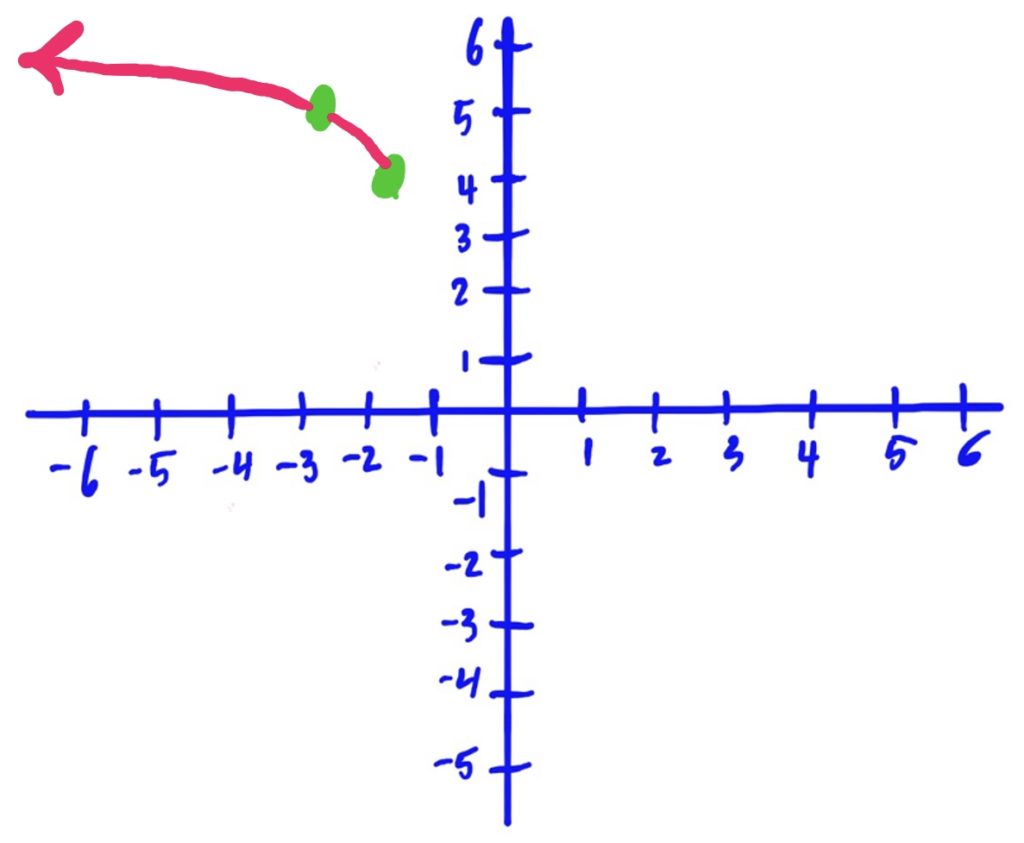
Library Function:\(f(x)=\sqrt{x}\)
Transformations Applied:
- Shifted right, then
- reflected over the \(y\)-axis, then
- shifted up 4
Library Function: \(f(x)=x^2\)
Transformations Applied:
- Scaled/stretched vertically by a factor of 5.
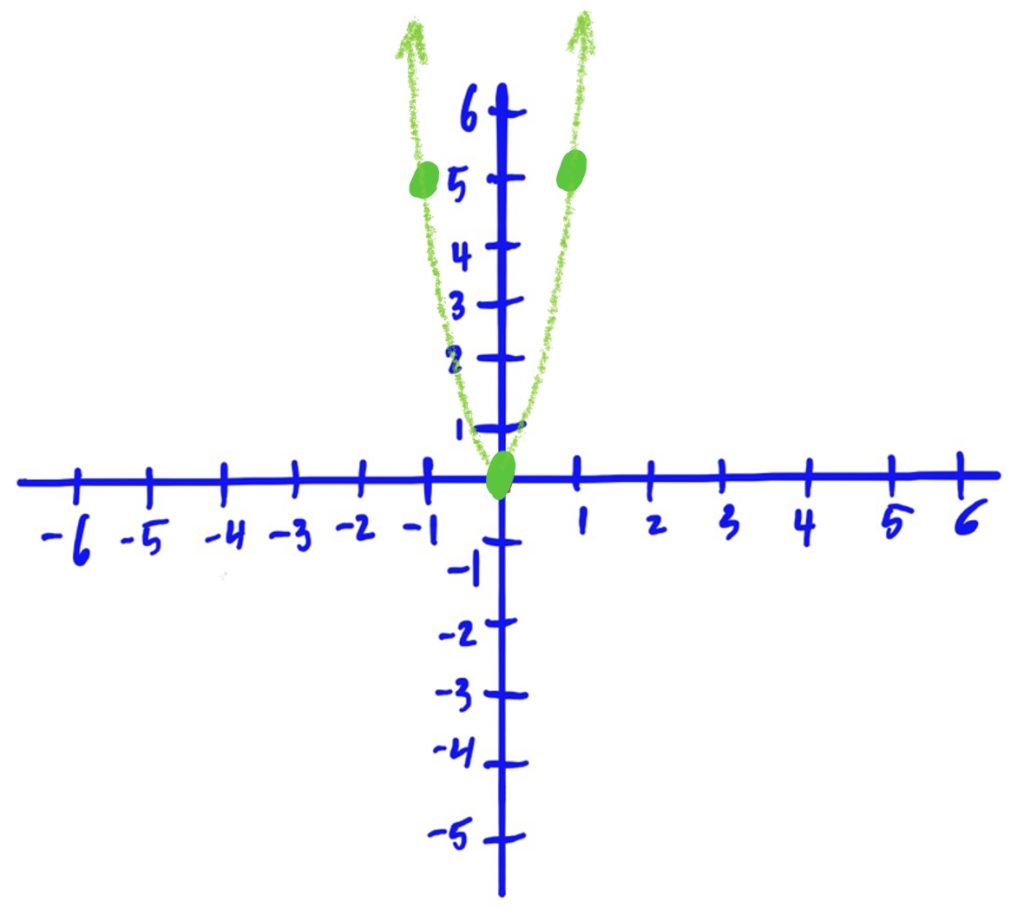
Library Function: \(f(x)=|x|\)
Transformations applied:
- scaled vertically by 3, then
- shifted up by 4
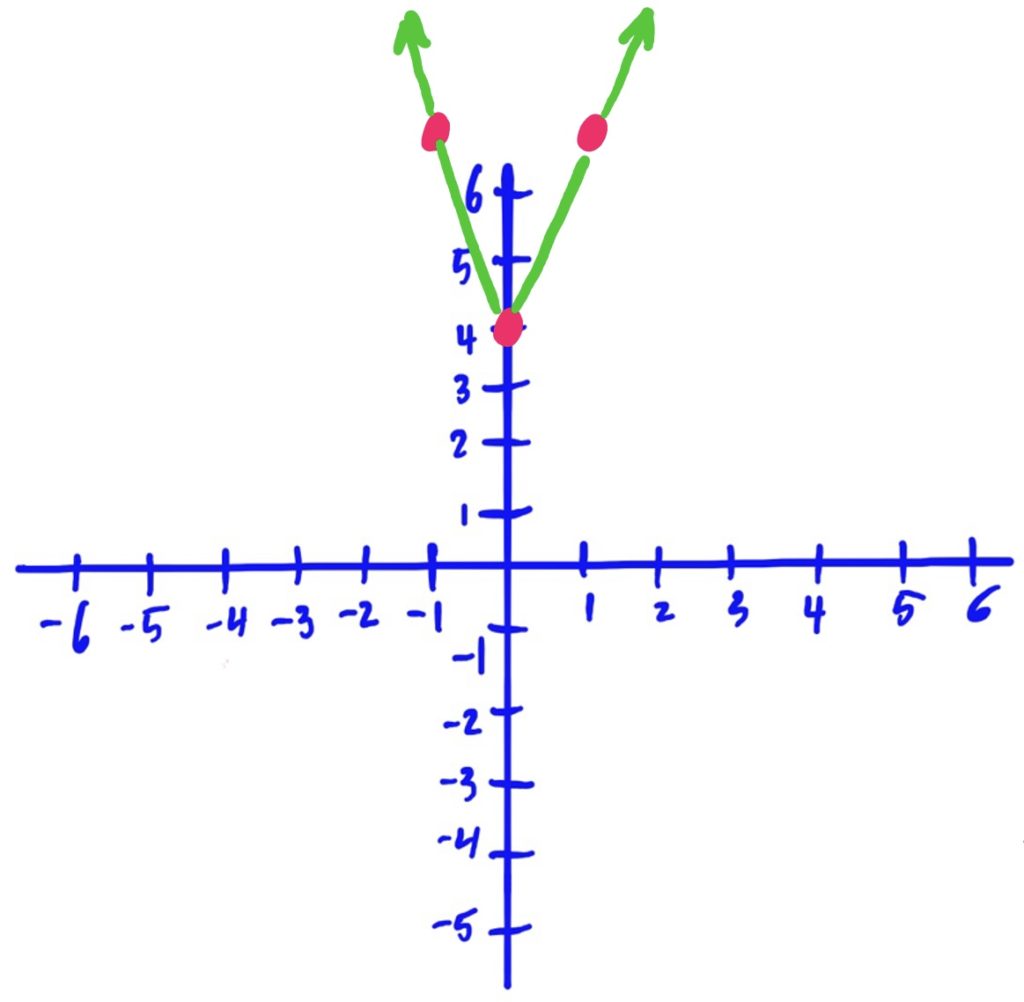
Library Function: \(f(x)=x^2\)
Transformations applied:
- Flipped vertically over \(y\)-axis, then
- scaled/stretched vertically by 2, then
- shifted up 3
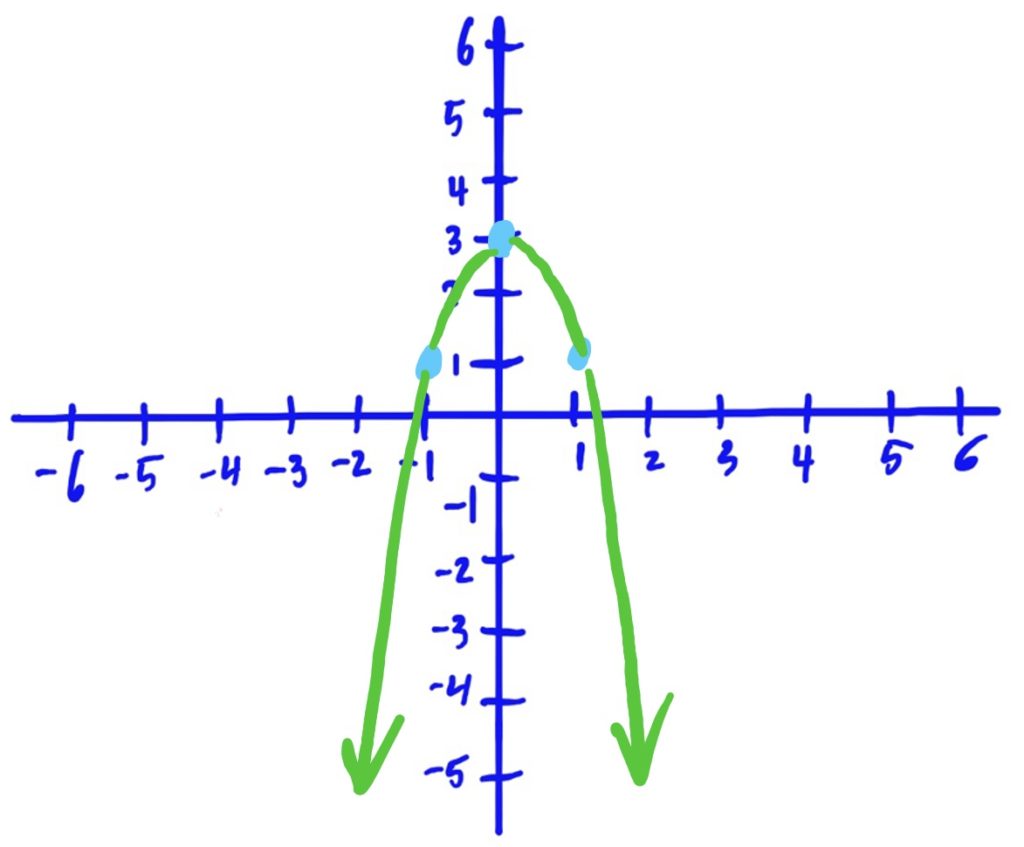
Library Function: \(f(x)=x^3\)
Transformations Applied:
- Shifted right by 3, then
- flipped horizontally over the \(y\)-axis, then
- flipped vertically over the \(x\)-axis, then
- scaled/stretched vertically by 2, then
- shifted up by 4.
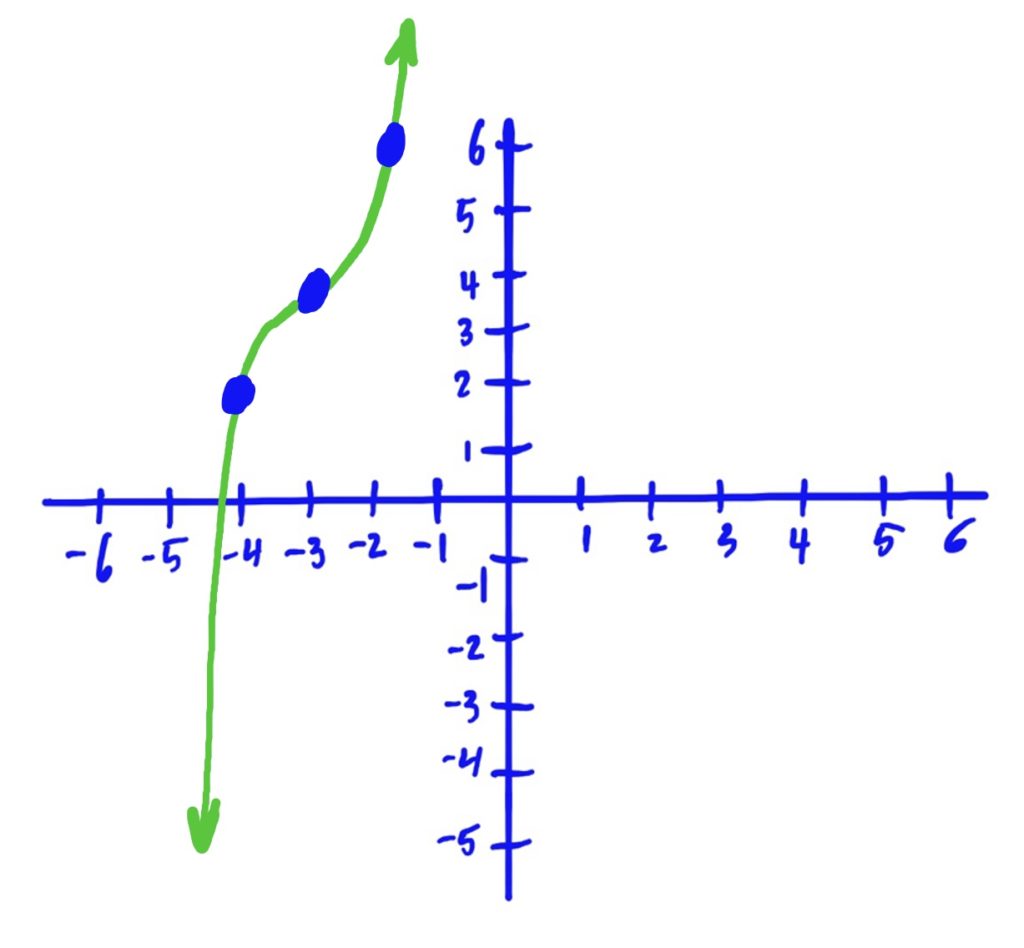
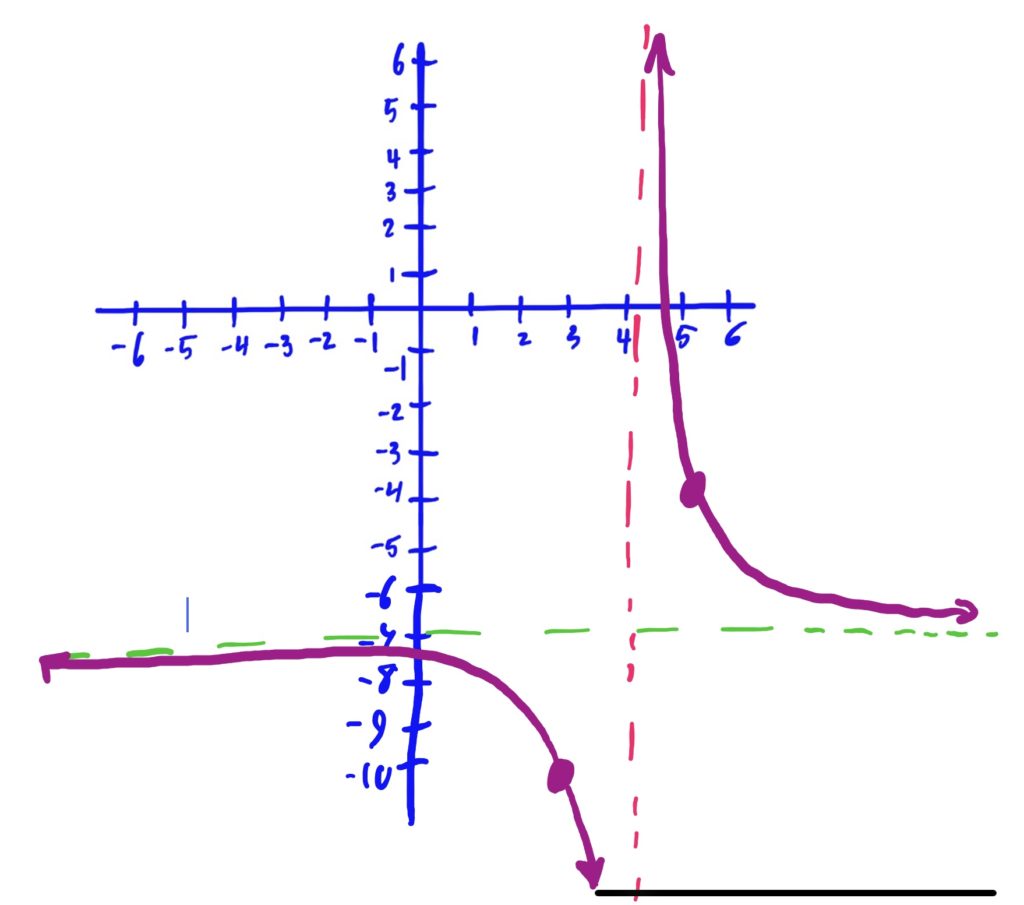
Library Function: \(f(x)=\frac{1}{x}\)
Transformations applied:
- Shifted to the left by 4, then
- flipped/reflected horizontally over the \(y\)-axis, then
- flipped vertically over the \(x\)-axis, then
- scaled/stretched vertically by 3, then
- shifted down 7.