Composing Functions Using Graphs
As mentioned in previous topics/lessons, function composition is the idea of taking one function’s output and feeding it immediately into another function as input.
No matter how functions are defined (typically) we can find the result of composing one with the other.
This includes graphs!
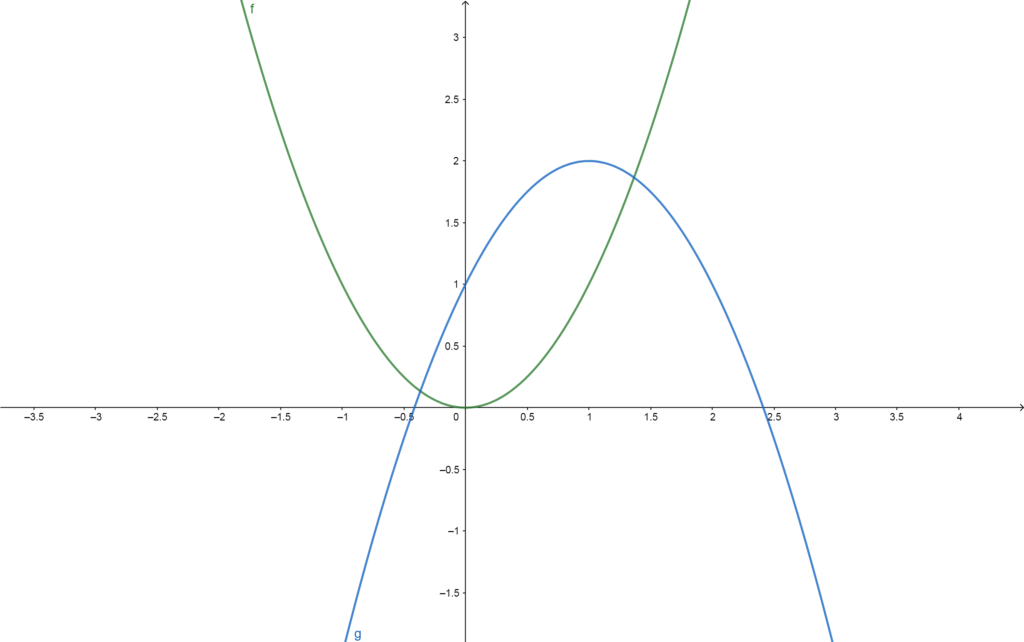
One can find the result of \(f(g(1))\) by first finding \(g(1)\) which is \(g(1)=2\) (as an estimate) and then plugging that immediately into \(f\) to get \(f(g(1))=f(2)=1\) (again, as an estimate).
One computes \(g(f(0))=g(0)=1\) because \(f(0)=0\). Just follow the graph, finding the \(y\)-values corresponding to \(x\)-values.
Thus, it doesn’t matter how two functions are defined. The idea of plugging the result of one function into another function as input remains exactly the same in all contexts.
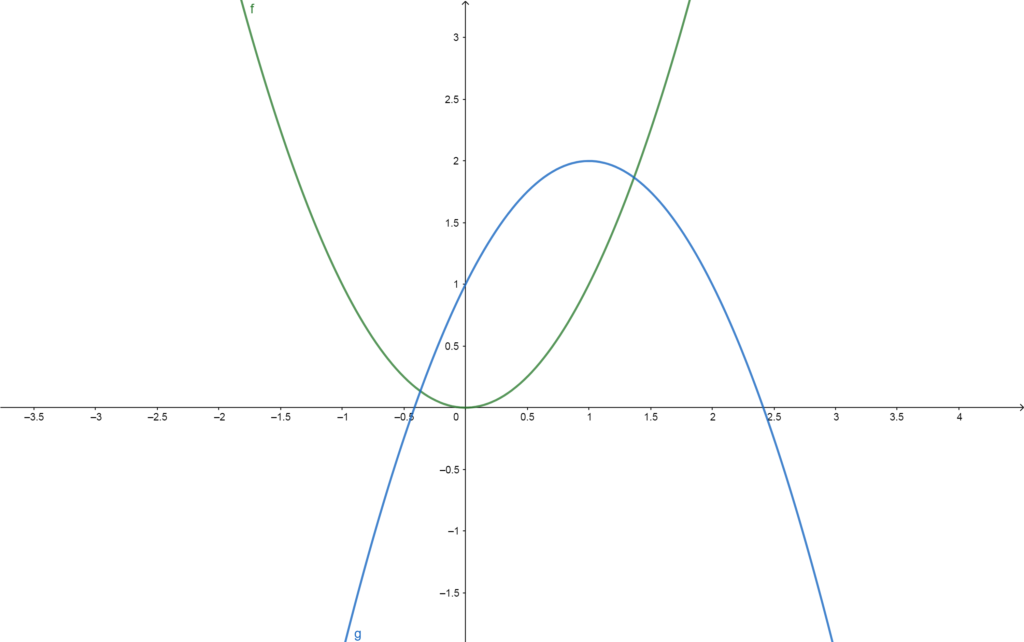
\(f(g(0))=f(1)=1\)
\(f(g(0.5))=f(1.75)=3\) (approximately)
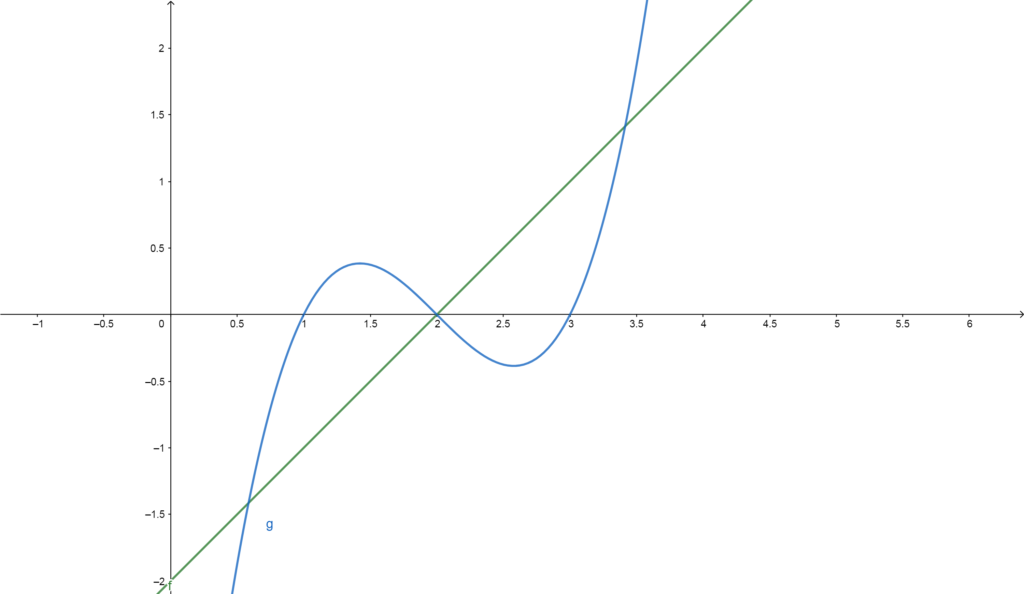
\(f(g(1))=f(0)=-2\)
\(f(g(1.5))=f(0.45)=-1.5\)
