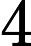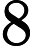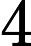In a manner of speaking, radicals can be “distributed” over products (i.e. stuff being multiplied). Similarly, reading the equation in reverse, the product of radicals/roots (when the roots are the same on the outside; i.e. have the same “power”) can be turned into one single radical with the inside stuff being multiplied within that radical.
We can use this ability to “distribute radicals,” along with the cancellation rule discussed in the previous lesson to help us reduce radicals of large composite (i.e. non-prime) numbers. The method that follows will help us reduce a radical like 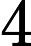
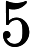
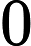




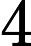
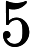
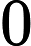





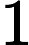
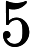




To illustrate, lets consider the following example: 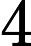
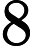



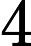
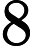





































































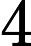




The above method works as well for powers of variables inside radicals. Just be careful to use absolute values when cancelling even radicals with even powers!
NOTE: You can certainly skip the “grouping the factors into powers corresponding to the root being taken” step (or at least simplify it a bit) by grouping the prime factors into powers of numbers that are evenly divisible by the power of the root, then dividing the power by the power of the root.