$Project Greater Ed Logo$

Negative Exponents and Cancellation

Precalculus Algebra Arithmetical Rules For Exponential Expressions Negative Exponents and Cancellation

A Few More Exponent Rules…

In other words, if you see a negative exponent, that means the exponential expression that has the negative exponent is in the “wrong part” of the fraction and should be moved to the “correct” part of the fraction.

This rule can be taken “by definition,” i.e not depending on other rules.

Notice: $5\cdot 6^{-3}=\frac{5}{6^3}$

The $6$ had a negative exponent, so we merely moved the $6^{-3}$ down to the denominator and turned the exponent positive, giving you what we have above. Note that the $5$ out in front did not move because it has a positive exponent. If you really wanted to, sure, you could move it to the denominator and make the exponent negative, but that doesn’t help with the problem.

Note: $\frac{3}{2^{-7}}=\frac{3}{1\cdot 2^{-7}}=\frac{3\cdot 2^7}{1}=3\cdot 2^7$.

In front of all numbers is always an implicit factor of $1$ (which we don’t typically write), hence what you see in the first step (which can be skipped if you understand why you can skip it). The $2$ has a negative exponent, so we brought it and its power up from the denominator to “where it belongs” in the numerator, and made the exponent positive, according to the rule. Note that we did nothing with the $3$ in the numerator because it has an (implicit) exponent of $1$, which is positive. So, it doesn’t need to move.

Note that $\frac{z^2y^{-3}}{3x^{-9}}=\frac{z^2x^9}{3y^3}$.

Here, we brought the $x^{-9}$ up to the numerator and turned the exponent positive, and brought the $y^{-3}$ down to the denominator and turned its exponent positive. The $z^2$ and the $3$ don’t change position because they didn’t have a negative exponent to begin with.

Note that, by how we interpret negative exponents, the $-3$ power indicates that everything on the inside of the parentheses is in the wrong part of the fraction. So we write

$$\begin{align}\left(\frac{x}{y}\right)^{-3}&=\frac{1}{\left(\frac{x}{y}\right)^3\\}&=\frac{1}{\frac{x^3}{y^3}}\\&=\frac{y^3}{x^3}\end{align}$$

The above is the simplified answer, but going one step further, pulling the power out of the fraction, we see that the above equals

$$\begin{align}\frac{y^3}{x^3}=\left(\frac{y}{x}\right)^3\end{align}$$

In summary, from the above we have that

$$\begin{align} \left(\frac{x}{y}\right)^{-3} &= \left(\frac{y}{x}\right)^3 \end{align}$$

This indicates that if you have a negative exponent on a fraction, you can flip the fraction on the inside, and change the power from negative to positive!

The last statement is the shortcut.

As always, it really doesn’t matter what sort of number you have in your exponent. Could be a decimal, fraction, complex number, etc. As long as you don’t end up somehow dividing by zero, if you want to change the sign of the exponent of an exponential expression, just move the expression to the opposite part of the fraction, then change the sign by negating it (i.e. if it was positive, make it negative, and vice versa).

In other words, when you have an exponential expression with the same base in the numerator and denominator, you can subtract the exponents, leaving the result in the numerator.

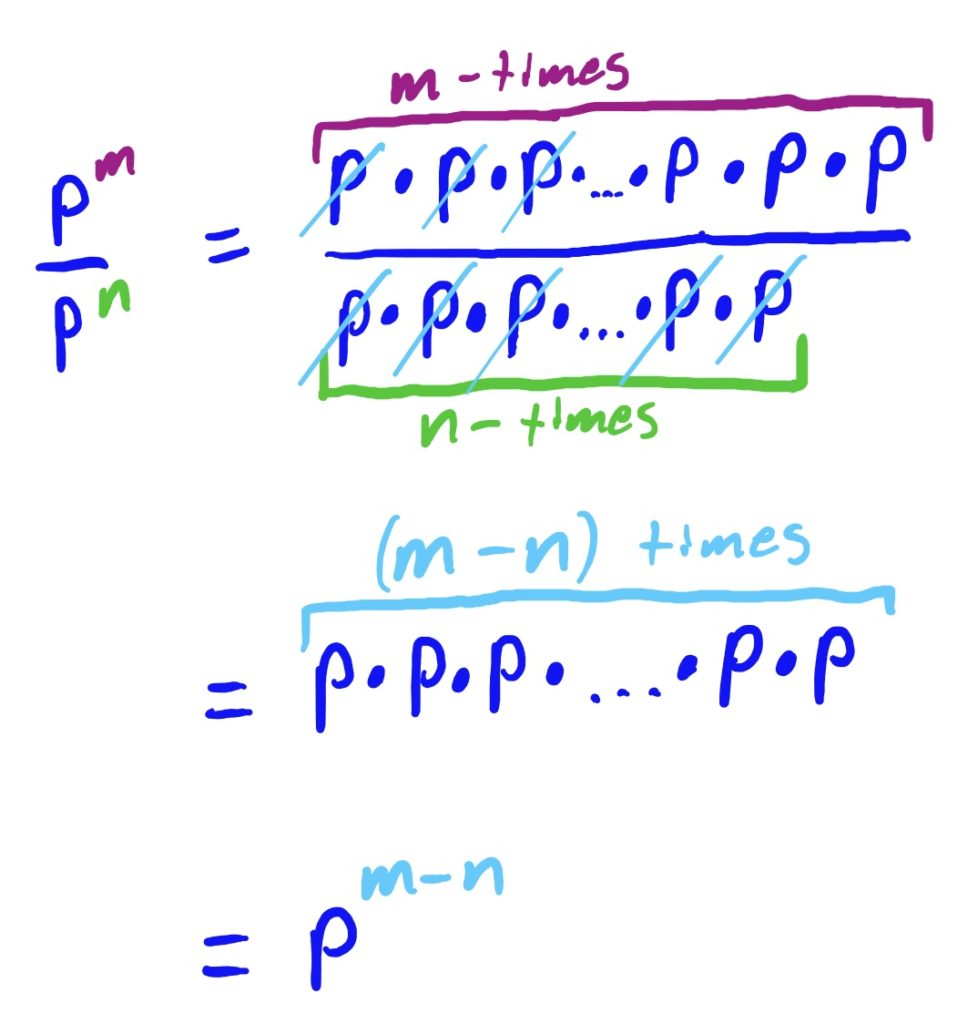
We know that if you have the same number in the numerator and denominator of a fraction, those numbers cancel out. So, leveraging how products of fractions work, we are able to cancel out a certain number of these repeated factors in the numerator and denominator. The exponents at the beginning essentially tell you how many of these factors you have in the top and in the bottom. The cancellation in the fraction above results in “taking away” the $m$ factors in the bottom from the $n$ in the top.

Using the rule, we have $\frac{2^7}{2^4}=2^{7-4}=2^3$.

To illustrate the “why” in the last box, notice:

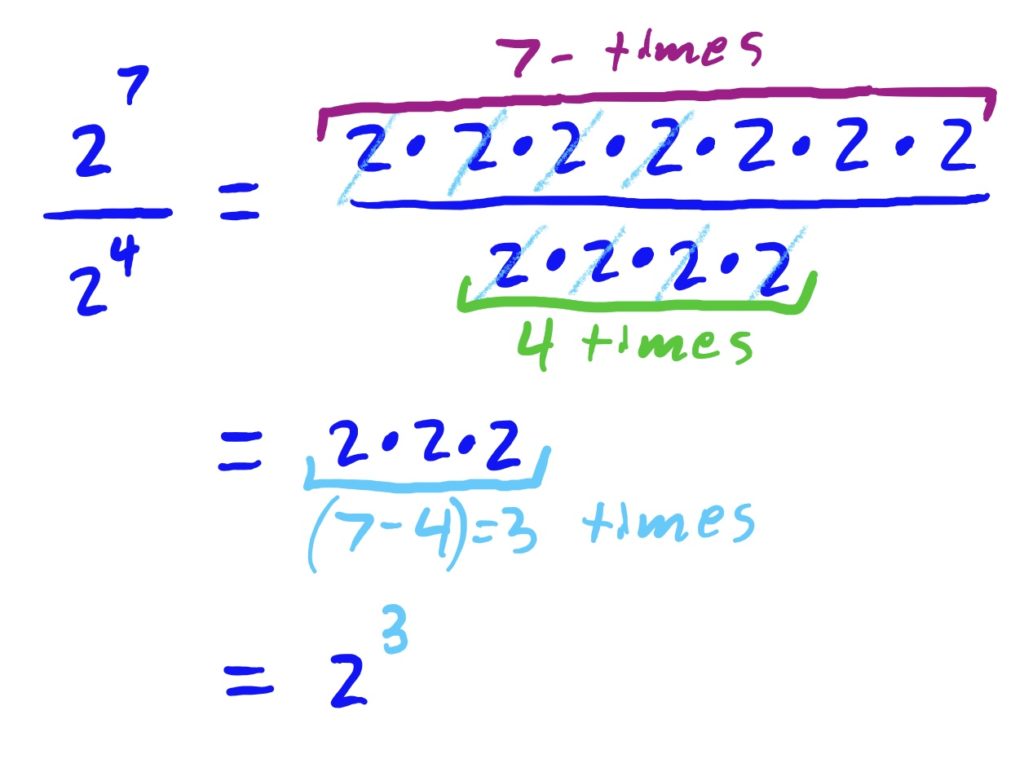
Specifically, since we have $7$ factors of $2$ in the numerator, and $4$ factors of $2$ in the denominator, we are able to cancel out all the denominator factors, leaving us with $3$ factors of $2$ in the numerator. This will always happen when you have more factors in the numerator than in the denominator; i.e. you will always have stuff remaining in the numerator (not in the denominator).

Using the rule, we get $\frac{5^3}{5^8}=5^{3-8}=5^{-5}=\frac{1}{5^5}$.

To illustrate why this works, notice

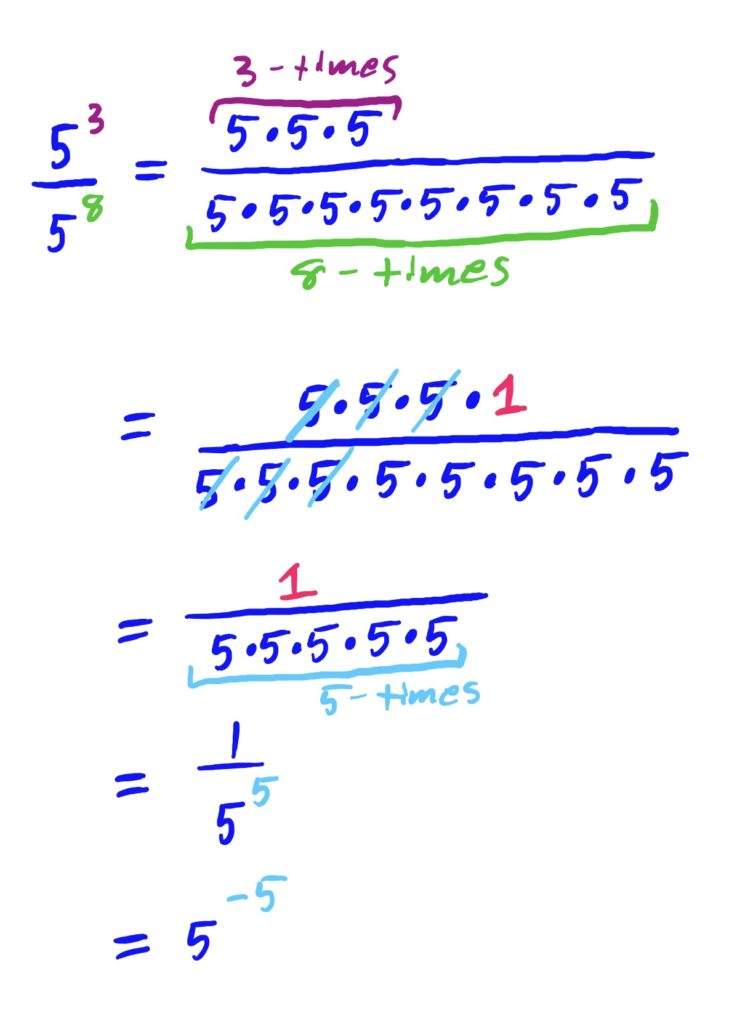
In this case, we have $3$ factors of $5$ in the numerator and $8$ factors of $5$ in the denominator. Cancelling everything we can, we annihilate all three factors in the numerator with three of the ones in the denominator. This cancellation has the effect of “taking away” factors (i.e. subtracting away factors, where the number of factors is indicated by each exponent). Since there are factors left in the denominator, we can either express this as a negative exponent, or in fraction form. Your choice.

This “subtract the exponent” rule works no matter what sort of number you have in the exponents of your numerator and denominator. Could be decimals, variables, fractions, negative numbers, and even complex numbers (i.e. numbers with $i$ in them).

Ex: $\frac{2^{-4.5}}{2^{\frac{1}{2}}}=2^{-4.5-\frac{1}{2}}=2^{-5}$

In this example, the rule didn’t change and we didn’t do any sleight of hand. Just blindly subtracted the exponents without really caring too much about what the exponents are.

This rule is more useful in settings where you have several factors on top and bottom and you’d like to cancel some of them. Viz $\frac{3\cdot x^8}{7\cdot x^3}$. This reduces as

$$\begin{align}\frac{3\cdot x^8}{7\cdot x^3}&=\frac{3}{7}\cdot \frac{x^8}{x^3}\\&=\frac{3}{7}\cdot x^5\end{align}$$.

Naturally, if you see that you have the same exponential expression in the top and bottom, you can cancel or subtract the exponents immediately. No need to break up the fraction like above. That is, you could just do

$$\begin{align}\frac{3\cdot x^8}{7\cdot x^3}&=\frac{3\cdot x^5}{7}\end{align}$$

which is the same as (read: equal to) the above.

In other words, if you have the same number of $x$’s being multiplied on the top and bottom, they can all be cancelled out, giving you only a 1. Naturally, this is because you have exactly the same thing/number in the numerator and denominator.

Note that this rule is merely a special case of the preceding rule. It is important enough to mention separately here.

Notice that you have exactly the same stuff in the numerator and denominator. Cancel out everything. Put another way, you have one number divided by itself. The result is $1$. So in a way, it doesn’t really matter what the exponents are here, does it?

Put yet another way, if you cancel everything over division, you are left with a 1.

The next example makes this idea a little less trivial.

Notice:

$$\begin{align}\frac{21\cdot 5^7}{13\cdot 5^7}&=\frac{21}{13}\cdot \frac{5^7}{5^7}\\&=\frac{21}{13}\cdot 1\\&=\frac{21}{13}\end{align}$$

Naturally, you can skip steps cancelling all at the beginning, not needing to break up the fraction into a product of two fractions. Viz:

$$\begin{align}\frac{21\cdot \not{5^7}}{13\cdot \not{5^7}}&=\frac{21\cdot 1}{13\cdot 1}\\&=\frac{21}{13}\end{align}$$

As with all exponent rules, it doesn’t matter if we are dealing with exponents with fractions, decimals, variables, or complex numbers. This cancellation rule applies (assuming the base is not zero). That is, you can totally have stuff like

$$\begin{align}\frac{3x^{7.142}}{5x^{7.142}}=\frac{3}{5}\end{align}$$

In summary, stuff with the same exponent in top and bottom cancels out completely.

$x^{-1}$ or $\frac{1}{x}$

Notice that $x^3\cdot x^{-4}=x^{3-4}=x^{-1}=\frac{1}{x}$, since negative exponents means that the exponential expression to which the exponent is attached is in the “wrong part” of the fraction. Moving the expression to the “correct part” of the fraction makes the exponent positive.

$\frac{y^3}{z^3x^2}$

In $\frac{y^3z^{-3}}{x^2}$, we have $z^{-3}$ with the negative exponent. Move this exponential expression down to the denominator (where it belongs) and change the sign of the exponent. That is all that is required here, since $y^3$ and $x^2$ both have positive exponents (so, they are in the “correct” part of the fraction).

$\frac{y^3}{x^4}$

The negative exponents means that the exponential expression to which they are attached are in the “wrong part” of the fraction. Moving them to the “correct part” of the fraction makes the exponents positive.

$\frac{2}{x^3y^2}$.

The $x$ was the only thing with a negative exponent, so it got moved to the denominator, and multiplied by the $y^2$ that was already there. The 2 in the numerator is not technically attached to the $x^{-3}$ since the 2 is out in front of it, so it stays in the numerator where it belongs.

$\frac{1}{x^{7}y^2}$

One could first write $\frac{x^{-7}}{y^2}=\frac{1\cdot x^{-7}}{y^2}$ (this step is helpful, but not necessary). Then, since we have a negative exponent on $x$, we can move the exponential expression $x^{-7}$ to the denominator (where it belongs) and make the exponent negative. The $1$ stays up top because that’s the only thing that is (technically) remaining. Everything else had a positive exponent, so it doesn’t need to move.

$\frac{1}{4m^6}$

The negative exponent on $(2m^3)^{-2}$ tells you to bring the whole parentheses down to the denominator. This gives you $\frac{1}{(2m^3)^2}$. Then, as per usual exponent rules, you can distribute that power of 2 to both the 2 and $m^3$, which will give you the final answer.

$v^{3}$

The negative exponent on the $v^{-7}$ and $v^{-10}$ indicates that both of these exponential expressions are in the wrong place of the fraction. Move them to the “correct” place and change their fractions to be positive. See the following for how this works out.

$$\begin{align} \frac{v^{-7}}{v^{-10}}&=\frac{v^{10}}{v^{7}}\end{align}$$

Now apply the subtraction/cancellation rule!

$$\begin{align}\frac{v^{10}}{v^{7}}&=v^{10-7}\\&=v^3\end{align}$$

$\frac{y^6}{x^4}$

The negative exponent on the whole fraction flips the fraction, changing the negative exponent to a positive one. Then, apply the exponent rule for fractions to get the result.

$$\begin{align} \left(\frac{x^2}{y^3}\right)^{-2} &=\left(\frac{y^3}{x^2}\right)^2\\&=\frac{y^6}{x^4}\end{align}$$

$x^6$

There are a few ways you could do this. When I see a fraction inside a negative power, that tells me to just flip the whole fraction inside the parentheses and make the power positive, then distribute the now positive power to each thing being multiplied (or divided, in some problems).

Alternatively, you can distribute the -3 power to both the stuff being multiplied in the numerator and denominator so you get $\frac{1^{-3}}{(x^2)^{-3}}=\frac{1}{x^{-6}}$ (because 1 to any power is 1). Then, you can simply bring the $x^{-6}$ up to the numerator where it belongs and make the exponent positive.

$z^{20.992}$

Alternatively, you can distribute the $-4.1$ power to both the stuff being multiplied in the numerator and denominator so you get $\frac{1^{-4.1}}{(z^2)^{-4.1}}=\frac{1}{z^{-20.992}}$ (because 1 to any power is 1). Then, you can simply bring the $x^{-20.992}$ up to the numerator where it belongs and make the exponent positive.

$\frac{9}{4x^{6}y^4}$

Distribute the power: $\left(\frac{2x^3}{3y^{-2}}\right)^{-2}=\frac{2^{-2}x^{-6}}{3^{-2}y^{4}}$
Put all exponential expressions with negative exponents in the correct part of the fraction: $\frac{2^{-2}x^{-6}}{3^{-2}y^{4}}=\frac{3^2}{2^2x^6y^4}$
Simplify to get $\frac{3^2}{2^2x^6y^4}=\frac{9}{4x^{6}y^4}$

$\frac{27y}{125\cdot x}$

Follow the steps you see below! (Note, some of the more obvious ones can be skipped)

$$\begin{align} \left(\frac{5x^\frac{1}{3}}{3y^{-\frac{1}{3}}}\right)^{-3} &=\frac{5^{-3}\cdot x^{-3}{3}}{3^{-3}\cdot y^{\frac{-3}{3}}}\\&=\frac{5^{-3}\cdot x^{-1}}{3^{-3}\cdot y^{-1}}\\&= \frac{27y}{125\cdot x} \end{align}$$

$x^2$

Simplify the expression by applying the definition of negative exponents repeatedly! Start with the stuff on the inside of the parentheses first. The “steps” are as follows:

$$\begin{align} \left(\frac{1}{\frac{1}{x^{-1}}}\right)^{-2} &=\left(\frac{1}{x}\right)^{-2}\\&=\frac{1}{x^{-2}}\\&=x^2\end{align}$$

Previous Topic

Back to Lesson

Next Lesson