$Project Greater Ed Logo$

Exponent Rules

Precalculus Algebra Arithmetical Rules For Exponential Expressions Exponent Rules

Mini Lecture Video

Exponent Rules

In other words, when the base is the same for two exponential expressions being multiplied, you add the exponents.

$$\begin{align} 2^4\cdot 2^5&=2^{4+5}\\&=2^9\end{align}$$

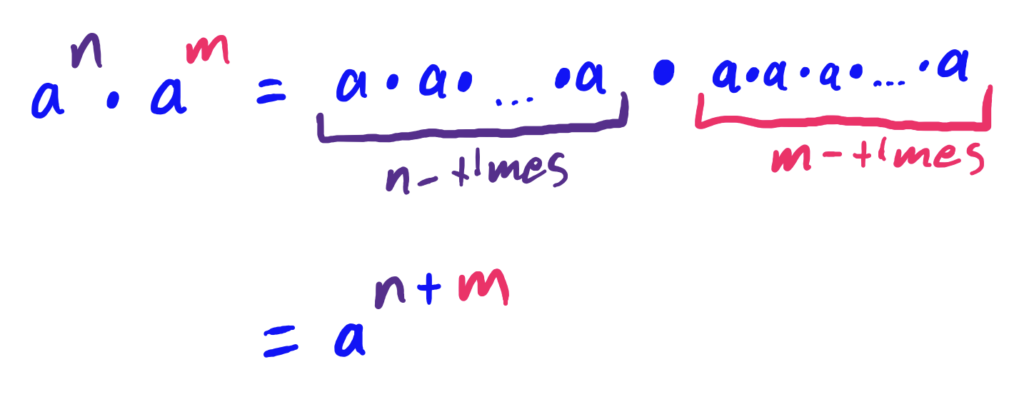
Exponentiation is repeated multiplication, so expanding out the exponential expressions and counting the number of $a$’s being multiplied gives us the result/rule.

This rule DOES NOT WORK when the bases of your exponential expressions are NOT the same. For instance, in the case of $3^5\cdot 2^7$ you CANNOT write $(3\cdot 2)^{12}$ or anything similar. In cases like these where the bases are different, YOU ARE STUCK AND CAN DO NOTHING!

This rule works even when you are multiplying several different terms. For example, $3^4\cdot 3^5\cdot 3^7=3^{16}$; again just adding exponents since the bases are the same.

This rule also works even if the exponents are weird, such as decimals or fractions or variables! In general, if bases are the same, you can add the exponents, no matter what they are!

When dealing with exponential expressions with coefficients (i.e. numbers out in front of the expression(s)) the numbers out in front get handled separately.

For example, to simplify the product $(3\cdot 2^4 )(7\cdot 2^5)$, multiply the coefficients separately from the exponential expressions, so you get $3\cdot 2^4 \cdot 7 \cdot 2^5=(3\cdot 7)\cdot 2^4\cdot 2^5=21\cdot 2^9$. The same idea should be applied when you have negative coefficients, or a minus sign out in front of one of your quantities.

In other words, when you have an exponent of an exponential expression, you multiply the exponents.

$$\begin{align}(a^3)^5&=a^{3\cdot 5}\\ a^{15}\end{align}$$

Inside the parentheses we have $n$ $a$’s being multiplied together, and the $m$ indicates how many of these groups of $n$ $a$’s we have. So, since we have $m$ groups of $n$ $a$’s, and everything is being multiplied, we must have a total of $m\cdot n$ $a$’s being multiplied.

s rule works no matter what $a$ and $b$ are. That is, $a$ and $b$ can be variables, decimals, fractions, etc. The rule works the same in all cases; just multiply the exponents, no matter what they are.

In other words, when you have two things being multiplied inside parentheses with an exponent on the outside, the exponent can be, in a sense, distributed to both factors.

$$\begin{align}(2x)^7&=2^7\cdot x^7\end{align}$$

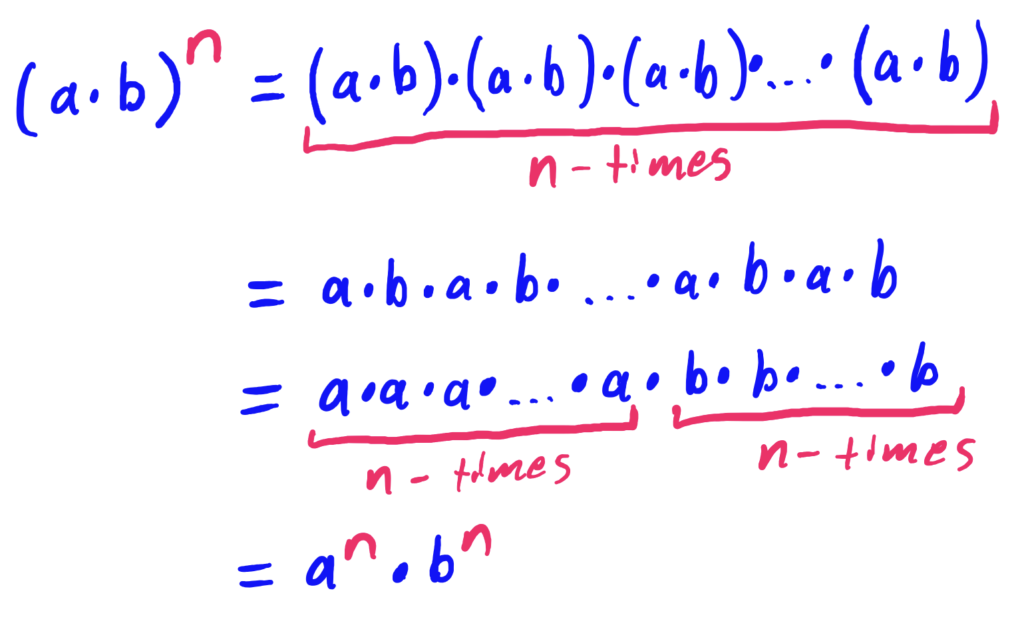
We have $n$ groups of $a\cdot b$’s, so that means we have a total of $n$ $a$’s and $n$ $b$’s being multiplied. Rearranging the multiplication so that the $a$’s and $b$’s are grouped gives us the rule.

This rule works no matter what $a$ and $b$ are. That is, $a$ and $b$ can be variables, decimals, fractions, etc. The rule works the same in all cases; just distribute the exponent to everything being multiplied inside the parentheses.

Also, this rule works even if you have several different factors being multiplied inside the parentheses, such as in $(2xy)^5$. In cases like these, you just “distribute” the power to each factor, so that $(2xy)^5=2^5x^5y^5$ and simplify where applicable.

In other words, when you have an exponent on a fraction, the exponent, in a sense, can be distributed to both whatever is in the numerator and whatever is in the denominator.

Caveat: $b\neq 0$ in the expression above, and $a$ and $n$ cannot simultaneously be zero. (See next rule for why this is the case)

$$\begin{align}\left(\frac{2}{3}\right)^5&=\frac{2^5}{3^5}\end{align}$$

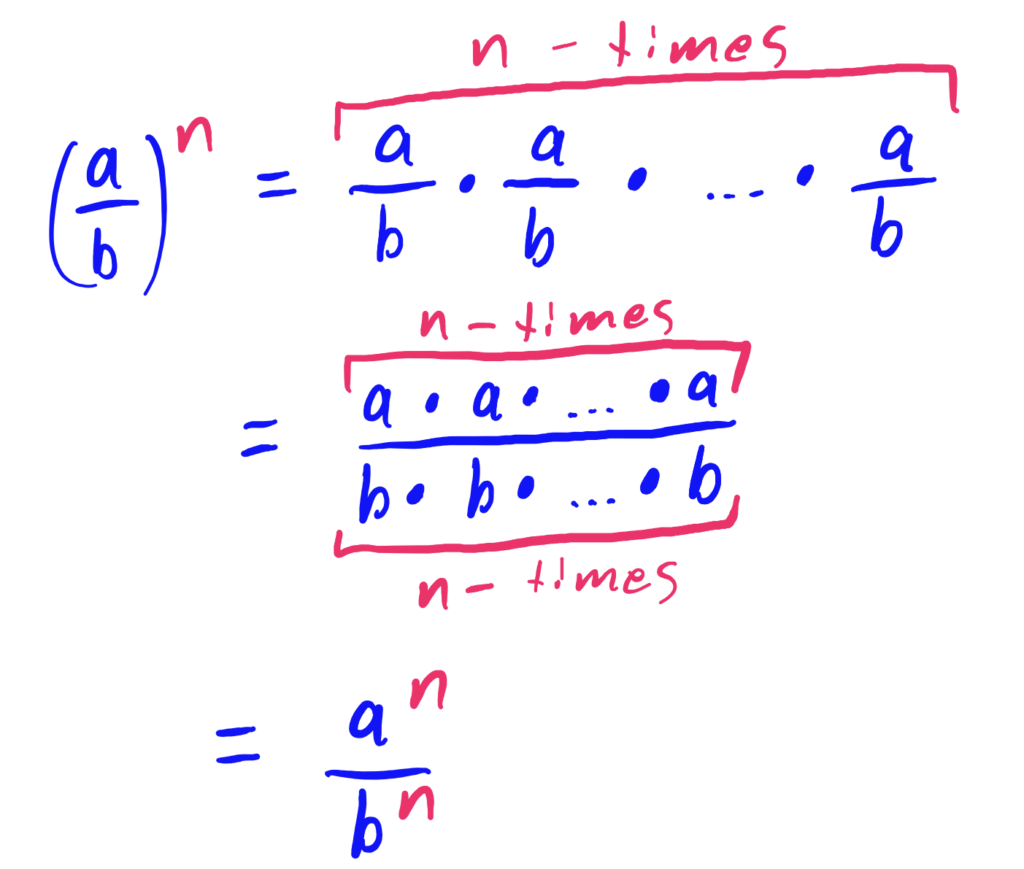
We have $n$ fractions being multiplied together. When you multiply fractions, you multiply straight across the numerator and denominator. Thus, we end up with $n$ $a$’s being multiplied in the numerator and $n$ $b$’s being multiplied in the denominator.

As usual, it (almost) doesn’t matter what $a$ and $b$ are. They could be decimals, variables, fractions, etc.

In other words, anything (but 0) to the 0th power is 1, no matter how complicated the expression for $a$ is.

IMPORTANT: If you have an expression that simplifies to $0^0$, then the expression is undefined.

$28391238^0=1$

$\left(\frac{4}{5}\right)^0=1$

Technically, this rule depends on how negative exponents work, which is covered in another lesson.

Let $a$ be any real number that is not $1$ nor $0$. Then note

$$\begin{align} 1&=\frac{a^2}{a^2}\\&=a^{2-2}\\&=a^0\end{align}$$

It might be more helpful to read the above in the reverse order.

Doesn’t matter what $a$ is, as long as $a\neq 0$. Could be a decimal, a fraction, some ugly weird expression, etc. Anything (except $0$) to the $0$th power is $1$… always.

In other words, anything to the first power is whatever you started with.

$134132^1=134132$. Nothing changes.

This rule works essentially by definition. We define powers of $1$ to work this way as a matter of convention.

This works no matter what $a$ is, as usual; it can be fractions, decimals, complex numbers, variables, etc. $a$ can even be $0$! No restriction. Anything to the first power is just itself.

Sometimes you will see problems like $x\cdot y^2\cdot x^2\cdot y^5$, asking you to simplify. There is no exponent on the first $x$. Implicitly, when you see no exponent on a variable or a number, technically the exponent is $1$.

It is sometimes helpful to write an exponent of $1$ in these sorts of situations because you know you are about to add exponents. Viz:

$$\begin{align}x\cdot y^2\cdot x^2\cdot y^5&=x^1\cdot y^2\cdot x^2\cdot y^5\\&=x^3\cdot y^7\end{align}$$.

Warning!

There is NO RULE for exponents of sums or differences!

For example, $(x+y)^n\neq x^n+y^n$ and $(x-y)^n=\neq x^n-y^n$

Try plugging in x=2, y=3, n=2 into both sides of these equations and you will see that the right hand side(s) DO NOT EQUAL the left-hand sides.So, when you see something like $(x+1)^2$, know that this is NOT EQUAL TO $x^2+1^2$. You’d have to FOIL $(x+1)^2$ to expand this expression!

$x^3\cdot x^4=x^7$

Simply add up the number of $x$’s being multiplied and write that number in the exponent of $x$.

$y^3\cdot y^4\cdot y=y^8$

There are 8 y’s being multiplied here. So we write $y^8$.

$x^5y^9$

Notice that there are a total of 5 $x$’s being multiplied, times a total of 9 $y$’s being multiplied. Since everything in sight is being multiplied, we can write $x^5y^9$ as our final answer.

$-20x^3y^4$.

Notice that everything in sight is being multiplied. Since we have some numbers being multiplied instead of only variables, we can multiply those directly, giving you the -20 part. Then, since we are also multiplying variables, we notice that there are 3 $x$’s total being multiplied and 4 $y$’s total being multiplied. So, putting this all together, we get the final answer.

$15.7x^2y^{3.67}$.

Multiply the coefficients $3.14$ and $5$ out front to get $15.7$. The first quantity $(3.14y)$ has no $x$-factor, so when this quantity is multiplied by the quantity $5x^2y^{2.67}$, the $x^2$ just comes along for the ride. However, since both quantities in parentheses have power-of-$y$ factors, we add the exponents on the $y$’s, giving the final answer.

$-4t^{11}$

There are two ways you can think to do this. The first is just noticing that everything in sight is being multiplied, so you multiply your coefficient numbers out in front of each exponential expression to get $-4$, and noticing that you have a total of 11 $t$’s being multiplied, and so write the final answer $-4 t^{11}$.

The other way is to first compute $(-2t^2)(-4t^3)=(8t^5)$, i.e. multiplying your first two parentheses, THEN multiplying that $(8t^5)$ and the remaining $-\frac{1}{2}t^6$ to get the final answer.

(Life/Math Tip!) This second method is a good general strategy when approaching complicated problems. Find a way to look at a smaller part of the problem, then work that out first, seeing how it contributes to the bigger problem’s solution. Odds are you know how to handle the simpler sub-problems.

$6^{20}$

Remember: when you have an exponent of another exponential expression, you can multiply the exponents.

$(-2)^4x^{12}$ or $16x^{12}$

In this case, you have two things being multiplied inside the exponential expression. The exponent gets “distributed” to both of those things. Since (-2) doesn’t have an exponent, you can compute $(-2)^4$ directly. Since $x$ has an exponent of 3, you multiply the 4 exponent with the 3 exponent to get the exponent 12.

$-3^4x^8y^{12}$ or $-81x^8y^{12}$

Since everything on the inside of the parentheses is being multiplied, you can distribute the power 4 to each factor inside (including the number 3). The negative is on the outside of the parentheses, so the power does not get applied to it.

$2^{\frac{1}{2}}x^3y^4$

Since everything on the inside of the parentheses is being multiplied, you can distribute the power $\frac{1}{2}$ to each factor inside (including the number 2). This gives you the following steps.

$\begin{align} (2x^6z^8)^{\frac{1}{2}}&=2^\frac{1}{2}(x^6)^{frac{1}{2}}(y^8)^\frac{1}{2}\\&=2^\frac{1}{2}x^\frac{6}{2}y^\frac{8}{2}\\&= 2^{\frac{1}{2}}x^3y^4\end{align}$

Note that in the second -to-last step we used the exponent rule.

$\frac{p^6}{q^{12}}$

Powers distribute to the entire top and bottom of fractions. So multiply the exponent of p by 3 and the exponent of q by 4 in both the numerator and denominator.

$\frac{27x^3}{p^6}$

Since everything is being either multiplied or divided, the power can be distributed to the 3, the x and the $p^2$. $3^3=27$, $(x^1)^3=x^3$ and $(p^2)^3=p^6$. Note carefully that what is in the numerator stays in the numerator, and what is in the denominator stays in the denominator!

$-\frac{x^5y^{10}}{z^{15}}$

This is similar to the last problem. Since everything is being multiplied or divided, the power 5 gets distributed to the $x$, the $y^2$ and the $z^3$. Multiply your exponents as usual.

$\frac{3.7^\frac{5}{2}x^5y^{\frac{15}{2}}}{z}$

This is similar to the last problem. Since everything is being multiplied or divided, the power 5 gets distributed to the $x$, the $y^2$ and the $z^3$. Multiply your exponents as usual.

$-\frac{25x^2z^6}{49y^6}$

A little more complicated, but basically the same as the last several examples. Since everything is being either multiplied or divided, just distribute the power to each number or power-of-variable.

-1. yup.

Since everything in parentheses is raised to the 0th power, all of that is equal to 1. Since there is a minus sign out in front of the parentheses, the 0 exponent doesn’t get applied to that, and so that minus sign just comes along for the ride, getting multiplied to that 1.

$\frac{(a+b)^5}{x^{15}}$. Yes, this is as simplified as it gets.

Notice that in the numerator we have $a+b$. By exponent rules, we can distribute the power 5 to both the ENTIRE numerator AS A WHOLE as well as the ENTIRE denominator AS A WHOLE. In the denominator, this gives you $x^15$ as usual, but the numerator cannot be simplified more because of the sum!

Earlier, we were able to distribute the outside power to everything on the inside (as a way of technically skipping steps) because everything in sight was being either multiplied or divided. Here, we are ADDING in the numerator, so we cannot have $a^5+b^5$ in the numerator. The best we can do for it is leaving it as $(a+b)^5$ unless you like to suffer through a lot of FOILing.

$\frac{(x-1)^6z^3}{p^9}$

Distribute the outermost power to the stuff either being multiplied or divided, as usual. You cannot distribute the power over the subtraction just like you can’t distribute it over addition. See the last problem for a thorough explanation for how these sorts of problems work.

$(x+1)^8(x-1)^{12}$

Powers distribute over multiplication and division only; not sums or differences. The only things being multiplied here are the $(x+1)^2$ and the $(x-1)^3$, so the the power 4 gets distributed to each of those two things. Multiply the exponents as usual.

Previous Lesson

Back to Lesson

Next Topic