Notations for Sets
Definition: Set
A Set is a collection of objects (called Elements).
Sets can contain (almost) anything you can think of; we are not just limited to letters and numbers. You can even have sets containing sets! There is no problem with this… unless you try to define a set containing all sets that don’t contain themselves. Then weird things happen (see Russell’s Paradox if curious).
NOTE: No matter how we notate sets, we will assume that sets do not contain duplicate elements.
Different Notations for Sets
Ex 1: \(\{2,4,6,8,10\}\)
Ex 2: \(\{1,3,5,…,11,13,15,17\}\)
Ex 3: \(\{1,2,3,4,5,…\}\)
Ex 4: \(\{…,-4,-2,0,2,4,6,…\}\)
Every element in the set is directly listed between curly braces. For economy of notation, when sets contain many (or infinitely many) elements and yet the pattern for what belongs in the set is clear, we can use ellipses “…” to say that the pattern continues either before, after, or between the elements listed.
Interval notation for sets is used when you want to define a set that contains a range of values on a number line; i.e. when you want to have a set containing every number (decimals and fractions included) between two endpoints on a number line.
We use square brackets “[” or “]” to indicate that we want to include the number at that endpoint in the set. We use round brackets “(” or “)” to indicate that we want to OMIT (or ‘leave out’) that endpoint so it is NOT in the set.
To represent an interval \([a,b)\) on a number line, first circle the endpoints \(a\) and \(b\), shading in the point if the endpoint is included (such as \(a\) in our case); otherwise, leave the point as an open circle. Then, shade the region between the endpoints.
Ex 1: \([0,1]\) represents all numbers between 0 and 1 (including all decimals and fractions), INCLUDING the endpoints 0 and 1. On a number line, this is represented as:
Ex 2: \([-4,3)\) represents all numbers between -4 and 3 (including all decimals and fractions), INCLUDING the endpoint -4 but NOT 3. On a number line, this is represented as:
Ex 3: \((0,6)\) represents all numbers between 0 and 6 (including all decimals and fractions), NOT INCLUDING the endpoints 0 and 6. On a number line, this is represented as:
Ex 4: \((1,\infty)\) represents all numbers greater than 1. On a number line, this is represented as:
Set Builder Notation is used when it is most convenient to define a set by describing the sort of elements it contains.
Anatomy of set-builder Notation via an example:
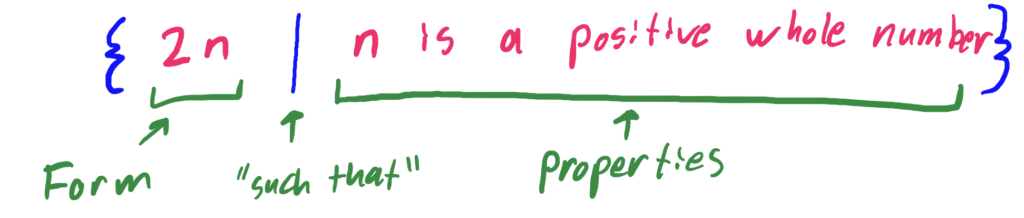
Verbally, the set above is defined to be “The set of all numbers of the form \(2n\) such that \(n\) is a positive whole number.”
The symbol(s) before the vertical bar “|” (some books use a colon “:” instead) designates the form of the elements of the set. The description after the “such that” symbol are the properties that the form has.
**To find specific examples of elements in your set: simply plug in different numbers (or symbols) that meet the requirements listed in the properties description.
In the case above, if you think about it, the set designated is the set of all positive even numbers!
Further Set Builder Examples
- \(\{3x|\ x\) is an integer (i.e. negative or nonnegative whole number)\(\}=\) the set of all numbers of the form \(3x\), where (or such that) \(x\) is an integer.
- This set is the set of all integers divisible by 3.
- \(\{a+b\sqrt{2}|\ a,b\) are real numbers\(\}=\) the set of all numbers of the form \(a+b\sqrt{2}\), such that \(a\) and \(b\) are real numbers (i.e. could be decimals or fractions).
- Examples of elements in this set: \(1+2\sqrt{2},\ 2.31-3\sqrt{2}, \frac{1}{2}+\frac{3}{4}\sqrt{2}, -82.481+6.71\sqrt{2}\).
- Note that the list above is not every element in the set. In fact, you couldn’t list all the elements of this set, even if you continuously wrote elements forever.
- \(\{1+2m|\ m\) is a positive whole number\(\}=\) the set of all numbers of the form \(1+2m\) where \(m\) is a positive whole number.
- If you plug in different values for \(m\) that meet the described property, then you will see that the above set is the set of all odd numbers!
Naming Sets
Just like numbers or other objects in mathematics, we can name sets using letters or other symbols. This is done by merely setting your choice of symbol equal to the set you wish to name.
For example, “Let \(S=\{1,3,5,6,7,9\}\)”.
So, any time we refer to the set \(S\) we are referring to the the set in curly braces above.
Special/Common Sets
There are a number of sets that are used so frequently that we give them special names. They are as follows.